The Wien’s bridge use in AC circuits for determining the value of unknown frequency. The bridge measures the frequencies from 100Hz to 100kHz. The accuracy of the bridges lies between 0.1 to 0.5 percent. The bridge is used for various other applications like capacitance measurement, harmonic distortion analyser and in the HF frequency oscillator.
The Wien’s bridge is frequency sensitive. Thereby, it is difficult to obtain the balance point in it. The input supply voltage is not purely sinusoidal, and they have some harmonics. The harmonics of the supply voltage disturbs the balance condition of the bridge. To overcome this problem the filter is used in the bridge. The filter connects in series with the null detector.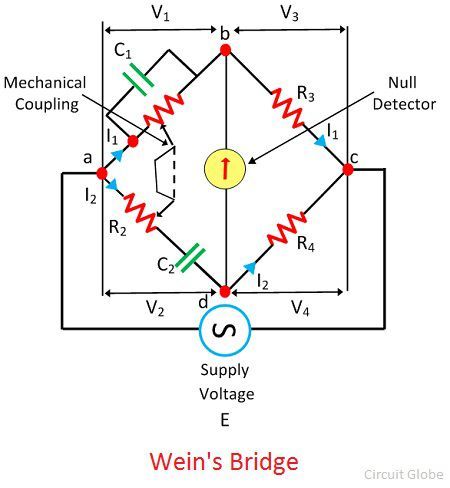
When the bridge is in the balanced condition, the potential of the node B and C are equal, i.e., the V1 = V2 and V3 = V4 The phase and the magnitude of V3 = I1R3 and V4 = I2R4 are equal, and they are overlapping each other. The current I1 flowing through the arm BD and the current I2 flowing through R4 is also in phase along with the I1R3 and I2R4.
The total voltage drop across the arm AC is equal to the sum of the voltage drop I2R2 across the resistance R2 and the capacitive drop I2/wC2 across the capacitance C2. When the bridge is in a balanced condition, the voltage V1 and V2 both are equals in magnitude and phase.
The phase of the voltage V1 and the voltage drop IRR1 across the arms R1 is also same. The resistance R1 is in the same phase as that of the voltage V1. The phasor sum of V1 and V3 or V2 and V4 will give the resultant supply voltage.
On equating the real part,
On comparing the imaginary part,
By substituting the value of ω = 2πf,
The slider of the resistance R1 and R2 mechanically connect to each other. So that, the R1 = R2 obtains.

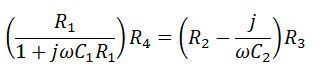
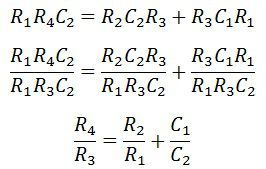

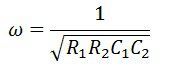
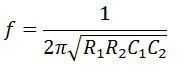
I have learned something…Thanks