Definition: The device uses for the measurement of minimum resistance with the help of comparison method is known as the Wheatstone bridge. The value of unknown resistance is determined by comparing it with the known resistance. The Wheatstone bridge works on the principle of null deflection, i.e. the ratio of their resistances are equal, and no current flows through the galvanometer. The bridge is very reliable and gives an accurate result.
In normal condition, the bridge remains in the unbalanced condition, i.e. the current flow through the galvanometer. When zero current passes through the galvanometer, then the bridge is said to be in balanced condition. This can be done by adjusting the known resistance P, Q and the variable resistance S.
The working of the bridge is similar to the potentiometer. The Wheatstone bridge is only used for determining the medium resistance. For measuring the high resistance, the sensitive ammeter is used in the circuit.
Construction of Wheatstone Bridge
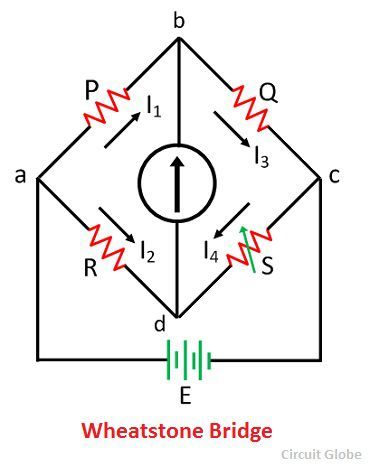
The basic circuit of the Wheatstone bridge is shown in the figure below. The bridge has four arms which consist two unknown resistance, one variable resistance and the one unknown resistance along with the emf source and galvanometer.
The emf supply is attached between point a and b, and the galvanometer is connected between point c and d. The current through the galvanometer depends on the potential difference across it.
Working of Galvanometer
The bridge is in balance condition when no current flows through the coil or the potential difference across the galvanometer is zero. This condition occurs when the potential difference across the a to b and a to d are equal, and the potential differences across the b to c and c to d remain same.
The current enters into the galvanometer divides into I1 and I2, and their magnitude remains same. The following condition exists when the current through the galvanometer is zero.
The bridge in a balanced condition is expressed as 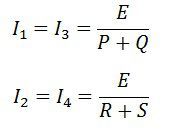
Where E – emf of the battery.
By substituting the value of I1 and 12 in equation (1) we get.
The equation (2) shows the balance condition of the Wheatstone bridge.
The value of unknown resistance is determined by the help of the equation (3). The R is the unknown resistance, and the S is the standard arm of the bridge and the P and Q are the ratio arm of the bridge.
Errors in Wheatstone Bridge
The following are the errors in the Wheatstone bridge.
- The difference between the true and the mark value of the three resistances can cause the error in measurement.
- The galvanometer is less sensitive. Thus, inaccuracy occurs in the balance point.
- The resistance of the bridge changes because of the self-heating which generates an error.
- The thermal emf cause serious trouble in the measurement of low-value resistance.
- The personal error occurs in the galvanometer by taking the reading or by finding the null point.
The above mention error can be reduced by using the best qualities resistor and galvanometer. The error because of self-heating of resistance can minimise by measuring the resistance within the short time. The thermal effect can also be reduced by connecting the reversing switch between the battery and the bridge.
Limitation of Wheat Stone Bridge
The Wheatstone bridge gives inaccurate readings if it is unbalanced. The Wheatstone bridge measures resistance from few ohms to megohms. The upper range of the bridge can be increased with the help of the applied emf, and the lower range is limited by connecting the lead at the binding post.
Sensitivity of the Wheatstone Bridge
The Wheatstone bridge is more sensitive when all their resistances are equal, or their ratio is unity. Their sensitivity decreases when their ratio is less than unity. The reduction in sensitivity reduces the accuracy of the bridge.

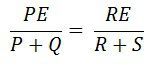


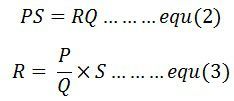
Wheatstone bridge also can be proved by Kirchoff’s law, you have chose easy method that’s great helpful to establish Wheatstone bridge thanks a lot.
I want to know how a circuit works?
thanks for your great support