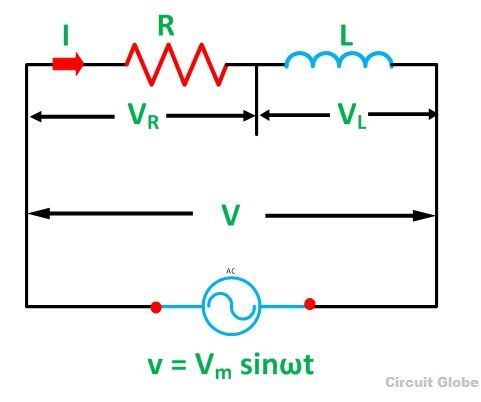
A circuit that contains a pure resistance R ohms connected in series with a coil having a pure inductance of L (Henry) is known as RL Series Circuit. When an AC supply voltage V is applied, the current, I flows in the circuit.
So, IR and IL will be the current flowing in the resistor and inductor respectively, but the amount of current flowing through both the elements will be same as they are connected in series with each other. The circuit diagram of RL Series Circuit is shown below:
- VR – voltage across the resistor R
- VL – voltage across the inductor L
- V – Total voltage of the circuit
Contents:
- Phasor Diagram of the RL Series Circuit
- Steps to draw the Phasor Diagram of RL Series Circuit
- Phase Angle
- Power in R L Series Circuit
- Waveform and Power Curve of the RL Series Circuit
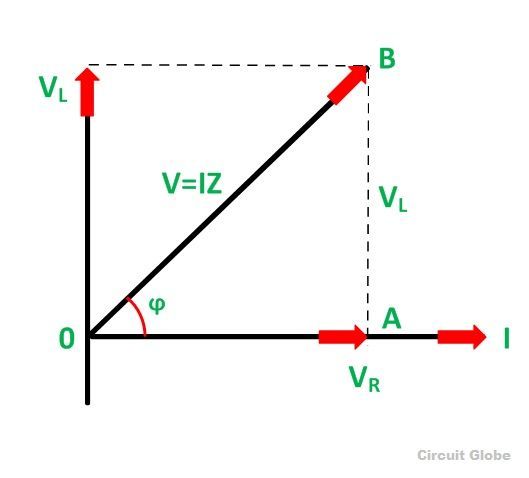
Phasor Diagram of the RL Series Circuit
The phasor diagram of the RL Series circuit is shown below:
Steps to draw the Phasor Diagram of RL Series Circuit
The following steps are given below which are followed to draw the phasor diagram step by step:
- Current I is taken as a reference.
- The Voltage drop across the resistance VR = IR is drawn in phase with the current I.
- The voltage drop across the inductive reactance VL =IXL is drawn ahead of the current I. As the current lags voltage by an angle of 90 degrees in the pure Inductive circuit.
- The vector sum of the two voltages drops VR and VL is equal to the applied voltage V.
Now,
In right-angle triangle OAB
VR = IR and VL = IXL where XL = 2πfL
Z is the total opposition offered to the flow of alternating current by an RL Series circuit and is called impedance of the circuit. It is measured in ohms (Ω).
Phase Angle
In RL Series circuit the current lags the voltage by 90 degrees angle known as phase angle. It is given by the equation: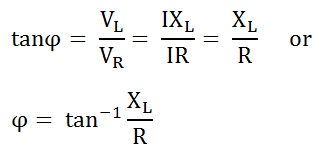
Power in R L Series Circuit
If the alternating voltage applied across the circuit is given by the equation: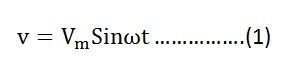
The equation of current I is given as: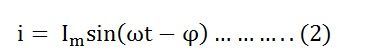
Then the instantaneous power is given by the equation:![]()
Putting the value of v and i from the equation (1) and (2) in the equation (3) we will get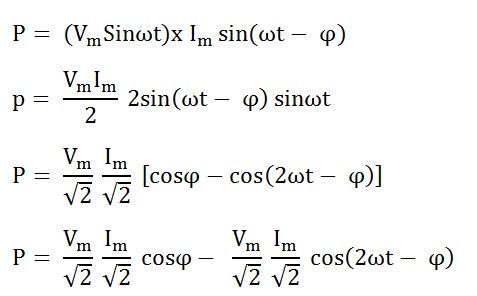
The average power consumed in the circuit over one complete cycle is given by the equation shown below: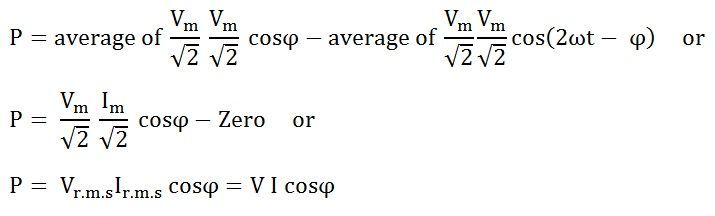
Where cosϕ is called the power factor of the circuit.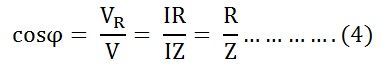
The power factor is defined as the ratio of resistance to the impedance of an AC Circuit.
Putting the value of V and cosϕ from the equation (4) the value of power will be:

From equation (5) it can be concluded that the inductor does not consume any power in the circuit.
Waveform and Power Curve of the RL Series Circuit
The waveform and power curve of the RL series circuit is shown below:
 The various points on the power curve are obtained by the product of voltage and current.
The various points on the power curve are obtained by the product of voltage and current.
If you analyze the curve carefully, it is seen that the power is negative between angle 0 and ϕ and between 180 degrees and (180 + ϕ) and during the rest of the cycle the power is positive. The current lags the voltage and thus they are not in phase with each other.


Nice explanation, thanks
Easy to understand
Thanks for answering
Helped a lot.. Thanks
Nice explanation….thanx
easy to understand
extremely helpful……very simple to understand, thank you:)
This is a nice site for AC Circuits.
thanks for this beautiful explanation
I have seen many videos but its not fruitful. After a struggle of half an hour, I found this site and it is extremely helpful and understandable. Appreciations.
Nicely explained 👌 I have solved my doubts by reading this. Thanx
Thank you so much for this explanation. After reading this all my confusions and doubts are clear.