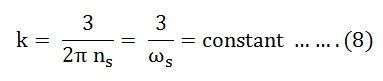The developed Torque or Induced Torque Equation in a machine is defined as the Torque generated by the electric to mechanical power conversion. The torque is also known as Electromagnetic Torque. This developed torque in the motor differs from the actual torque available at the terminals of the motor, which is almost equal to the friction and windage torques on the machine.
The developed torque equation is given as:
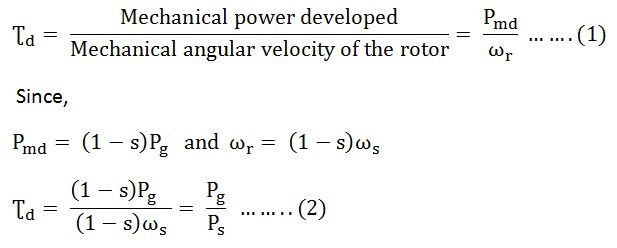 The above equation expresses the developed torque directly in terms of the air gap power Pg and the synchronous speed ωs. Since ωs is constant and independent of the load conditions. If the value of the Pg is known then, the developed torque can be found directly. The air gap power Pg is also called as the Torque in Synchronous Watts.
The above equation expresses the developed torque directly in terms of the air gap power Pg and the synchronous speed ωs. Since ωs is constant and independent of the load conditions. If the value of the Pg is known then, the developed torque can be found directly. The air gap power Pg is also called as the Torque in Synchronous Watts.
Synchronous Watt is the torque that develops the power of 1 Watt when the machine is running at synchronous speed.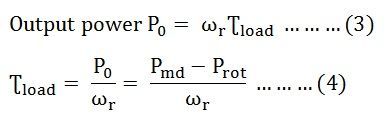
Now, the electrical power generated in the rotor is given by the equation shown below: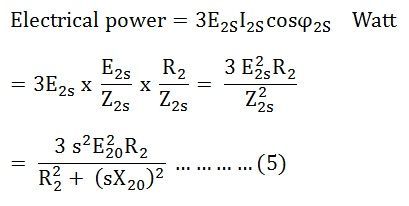
These electrical powers are dissipated as I2R losses or copper loss in the rotor circuit.
Input power to the rotor is given as:
Starting Torque Of Induction Motor
At the start condition the value of s = 1. Therefore, the starting is obtained by putting the value of s = 1 in the equation (6), we get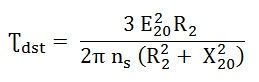
The starting torque is also known as the Standstill Torque.
Torque Equation at Synchronous Speed
At synchronous speed, s = 0 and hence developed torque Ʈd = 0. At synchronous speed, developed torque is zero.
Since E1 is nearly equal to V1 the equation (12) becomes
The Starting torque is obtained by putting, s = 1 in equation (13)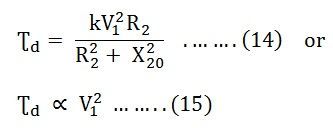
Hence, it is clear from the above equation that the starting torque is proportional to the square of the stator applied voltage.
Also See: Maximum Torque Condition of an Induction Motor