When a DC machine is loaded either as a motor or as a generator, the rotor conductors carry current. These conductors lie in the magnetic field of the air gap.
Thus, each conductor experiences a force. The conductors lie near the surface of the rotor at a common radius from its centre. Hence, a torque is produced around the circumference of the rotor, and the rotor starts rotating.
When the machine operates as a generator at a constant speed, this torque is equal and opposite to that provided by the prime mover.
When the machine is operating as a motor, the torque is transferred to the shaft of the rotor and drives the mechanical load. The expression is the same for the generator and motor.
When the current-carrying current is placed in the magnetic field, a force is exerted or it which exerts turning moment or torque F x r. This torque is produced due to the electromagnetic effect, hence is called Electromagnetic torque.
The torque which is produced in the armature is not fully used at the shaft for doing the useful work. Some part of it gets lost due to mechanical losses. The torque which is used for doing useful work in known as the shaft torque.
Since,
Multiplying the equation (1) by Ia we get
Where,
VIa is the electrical power input to the armature.
I2aRa is the copper loss in the armature.
We know that,
Total electrical power supplied to the armature = Mechanical power developed by the armature + losses due to armature resistance
Now, the mechanical power developed by the armature is Pm,
Also, the mechanical power that rotates the armature can be given regarding torque T and speed n.
Where n is in revolution per seconds (rps) and T is in Newton-Meter.
Hence,
But,
Where N is the speed in revolution per minute (rpm) and
Where n is the speed in (rps).
Therefore,
So, the torque equation is given as:
For a particular DC Motor, the number of poles (P) and the number of conductors per parallel path (Z/A) are constant.
Where
Thus, from the above equation (5) it is clear that the torque produced in the armature is directly proportional to the flux per pole and the armature current.
Moreover, the direction of electromagnetic torque developed in the armature depends upon the current in armature conductors. If either of the two is reversed the direction of torque produced is reversed and hence the direction of rotation. But when both are reversed, and direction of torque does not change.

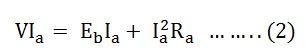
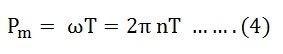
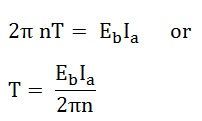
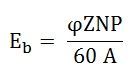
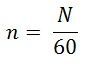
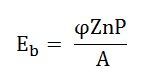
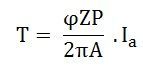
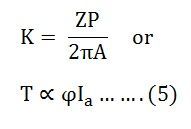
EXCELLENT EXPLANATION …I LIKE VERY MUCH
Excellent English ..I like very much
How does commutator keep armature flux stationary in spite rotation?
Sir applications tell me also…?plz
The DC motors are used in the fan, blower, centrifugal pumps, trolleys, cars, rolling mills, ice machines etc.
Very nice explanation…..thanks.
VERY GOOD EXPLANATION
Thank you sir. Very well explained. 🙏🙏🙏🙏🙏