Definition: Load equalisation is the process of smoothing the fluctuating load. The fluctuate load draws heavy current from the supply during the peak interval and also cause a large voltage drop in the system due to which the equipment may get damage. In load equalisation, the energy is stored at light load, and this energy is utilised when the peak load occurs. Thus, the electrical power from the supply remains constant.
The load fluctuation mostly occurs in some of the drives. For example, in a pressing machine, a large torque is required for a short duration. Otherwise, the torque is zero. Some of the other examples are a rolling mill, reciprocating pump, planning machines, electrical hammer, etc.
In electrical drives, the load fluctuation occurs in the wide range. For supplying the peak torque demand to electrical drives the motor should have high ratings, and also the motor will draw pulse current from the supply. The amplitude of pulse current gives rise to a line voltage fluctuation which affected the other load connected to the line.
Method of Load Equalisation
The problem of load fluctuation can be overcome by using the flywheel.The flying wheel is mounted on a motor shaft in non-reversible drives. In variable speed and reversible drive, a flywheel cannot be mounted on the motor shaft as it will increase the transient time of the drive. If the motor is fed from the motor generator set, then flywheel mounted on the motor generator shaft and hence equalises the load on the source but not load on the motor.
When the load is light, the flywheel accelerated and stored the excess energy drawn from the supply. During the peak load, the flying wheel decelerates and supply the stored energy to the load along with the supply energy. Hence the power remains constant, and the load demand is reduced.
Moment of inertia of the flying wheel required for load equalisation is calculated as follows. Consider the linear motor speed torque curve as shown in the figure below.
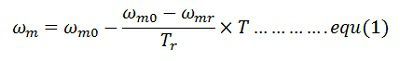 Assumed the response of the motor is slow due to large inertia and hence applicable for transient operation. Differentiate the equation (1) and multiply both sides by J (moment of inertia).
Assumed the response of the motor is slow due to large inertia and hence applicable for transient operation. Differentiate the equation (1) and multiply both sides by J (moment of inertia).
 Where Τm is the mechanical time constant of the motor. It is the time required for the motor speed to change by (ωm0 – ωm) when motor torque is maintained constant at rated value ᴛr. From equation(2) and (3)
Where Τm is the mechanical time constant of the motor. It is the time required for the motor speed to change by (ωm0 – ωm) when motor torque is maintained constant at rated value ᴛr. From equation(2) and (3)
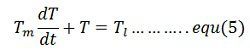 Consider a periodic load torque a cycle which consists of one high load period with torque Tlh and duration the, and one light load period with torque Tll and duration tl
Consider a periodic load torque a cycle which consists of one high load period with torque Tlh and duration the, and one light load period with torque Tll and duration tl
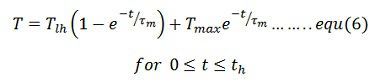 Where Tmin is the motor torque at t = 0 which is also the instant when heavy load Tlh is applied. If motor torque at the end of heavy load period is Tmax, then from the equation (6)
Where Tmin is the motor torque at t = 0 which is also the instant when heavy load Tlh is applied. If motor torque at the end of heavy load period is Tmax, then from the equation (6)
![]() Solution of equation (5) for the light load period with the initial motor torque equal to Tmax is
Solution of equation (5) for the light load period with the initial motor torque equal to Tmax is
When operating at steady state the motor torque at the end of a cycle will be the same as at the beginning of a cycle.Hence at t’ = tl, T = tmin. Substituting in equation (8) give
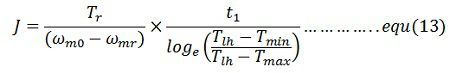 Moment of inertia of the flywheel required can be calculated either from equation(11) and (12)
Moment of inertia of the flywheel required can be calculated either from equation(11) and (12)
![]() Where W is the weight of the wheel (Kg), and R is the radius (m).
Where W is the weight of the wheel (Kg), and R is the radius (m).
Note: The moment of inertia is the angular obstruction of the rotating body. It is the product of the mass and a square of a distance from the axis of rotation.

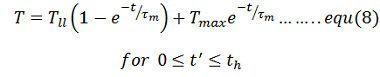
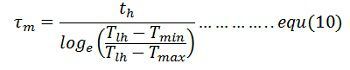
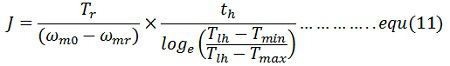
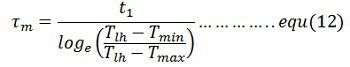
Thanks for the brief knowledge.