When the motor rotates, the load of the system may rotate or may go through a translational motion. In the translational motion, the position of the body changes from point to point in space.The speed of the load may be different from that of the motor.
If the load has different parts, their speed may be different. Some part of the rotor may rotate while others may go through a translational motion. The equivalent load system of the motor is shown in the figure below.
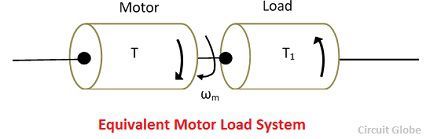 Where J – the polar moment of inertia of motor-load system, referred to the motor shaft, kg-m2
Where J – the polar moment of inertia of motor-load system, referred to the motor shaft, kg-m2
ωm – instantaneous angular velocity of the motor shaft, rad/sec.
T – the instantaneous value of developed motor torque, N-m.
T1 – the instantaneous value of load torque, referred to a motor shaft, N-m.
The equation shown below described the motor load equation.This equation is applicable for variable inertia drives such as mine, winders, reel, drives, industrial robots. In this equation, the load torque includes friction and windage torque of the motor.
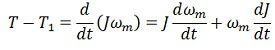 For constant inertia drive dj/dt = 0. Therefore the equation becomes
For constant inertia drive dj/dt = 0. Therefore the equation becomes
![]() The above equation shows that the load developed by the motor is counter-balanced by a load torque T1 and a dynamic torque jdωmt/dt.The torque component j(dωmt/dt) is called dynamic torque because it is present only during transient operations.
The above equation shows that the load developed by the motor is counter-balanced by a load torque T1 and a dynamic torque jdωmt/dt.The torque component j(dωmt/dt) is called dynamic torque because it is present only during transient operations.
The acceleration or deacceleration of the drive mainly depends on whether the load torque is greater or less than the motor torque. During acceleration, the motor supplies the load torque along with an additional torque component jdωmt/dt to overcome the drive inertia.
The drives which have a large inertia must increase the load torque by a large amount for getting sufficient acceleration. The drive which requires a fast transient response, their motor torque should be maintained at the excessive value and motor load system should be designed with a lower possible inertia.
The energy associated with dynamic torque is stored in the form of kinetic energy and given by the equation jdω2m/dt. During the deacceleration, the dynamic torque has a negative sign. Thus it assists the motor developed torque T and maintains the drive motion by extracting energy from stored kinetic energy.
