When the transformer is on the loaded condition, the secondary of the transformer is connected to load. The load can be resistive, inductive or capacitive. The current I2 flows through the secondary winding of the transformer. The magnitude of the secondary current depends on the terminal voltage V2 and the load impedance. The phase angle between the secondary current and voltage depends on the nature of the load.
Contents:
- Operation of the Transformer on Load Condition
- Phasor Diagram of Transformer on Inductive Load
- Steps to draw the phasor diagram
- Phasor Diagram of Transformer on Capacitive Load
- Steps to draw the phasor diagram at capacitive load
Operation of the Transformer on Load Condition
The Operation of the Transformer on Load Condition is explained below:
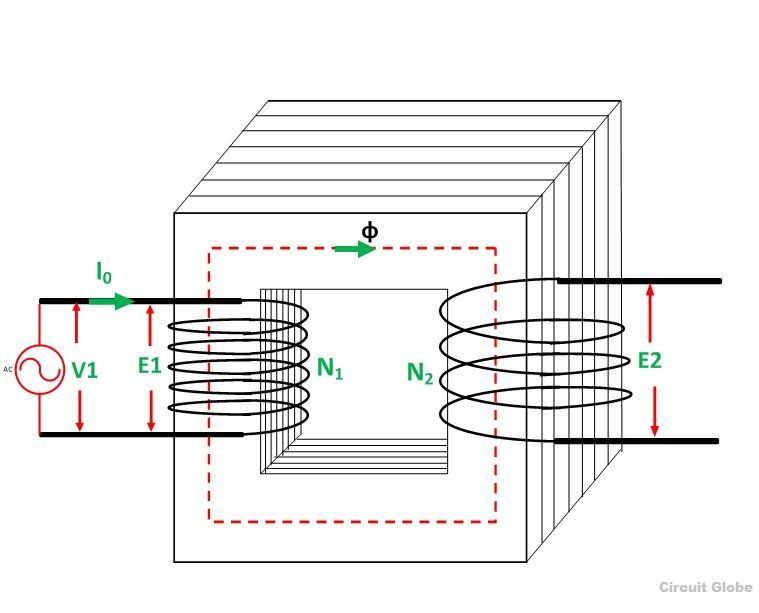
- When the secondary of the transformer is kept open, it draws the no-load current from the main supply. The no-load current induces the magnetomotive force N0I0 and this force set up the flux Φ in the core of the transformer. The circuit of the transformer at no load condition is shown in the figure below:
- When the load is connected to the secondary of the transformer, I2 current flows through their secondary winding. The secondary current induces the magnetomotive force N2I2 on the secondary winding of the transformer. This force set up the flux φ2 in the transformer core. The flux φ2 opposes the flux φ, according to Lenz’s law.
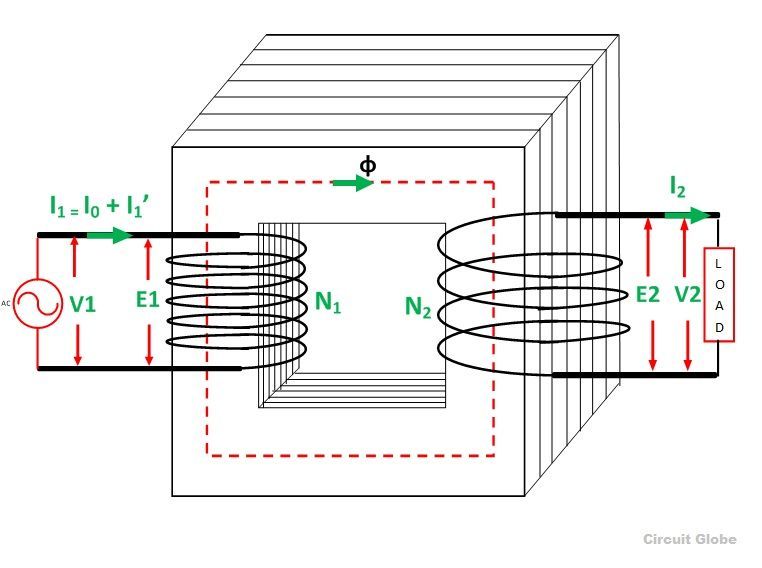
- As the flux φ2 opposes the flux φ, the resultant flux of the transformer decreases and this flux reduces the induced EMF E1. Thus, the strength of the V1 is more than E1 and an additional primary current I’1 drawn from the main supply.
The additional current is used for restoring the original value of the flux in the core of the transformer so that V1 = E1. The primary current I’1 is in phase opposition with the secondary current I2. Thus, it is called the primary counter-balancing current. - The additional current I’1 induces the magnetomotive force N1I’1. And this force set up the flux φ’1. The direction of the flux is the same as that of the φ and it cancels the flux φ2 which induces because of the MMF N2I2
- As the flux φ2 opposes the flux φ, the resultant flux of the transformer decreases and this flux reduces the induced EMF E1. Thus, the strength of the V1 is more than E1 and an additional primary current I’1 drawn from the main supply.
- When the load is connected to the secondary of the transformer, I2 current flows through their secondary winding. The secondary current induces the magnetomotive force N2I2 on the secondary winding of the transformer. This force set up the flux φ2 in the transformer core. The flux φ2 opposes the flux φ, according to Lenz’s law.
- The phase difference between V1 and I1 gives the power factor angle ϕ1 of the primary side of the transformer.
- The power factor of the secondary side depends upon the type of load connected to the transformer.
- If the load is inductive as shown in the above phasor diagram, the power factor will be lagging, and if the load is capacitive, the power factor will be leading. The total primary current I1 is the vector sum of the currents I0 and I1’. i.e
Phasor Diagram of Transformer on Inductive Load
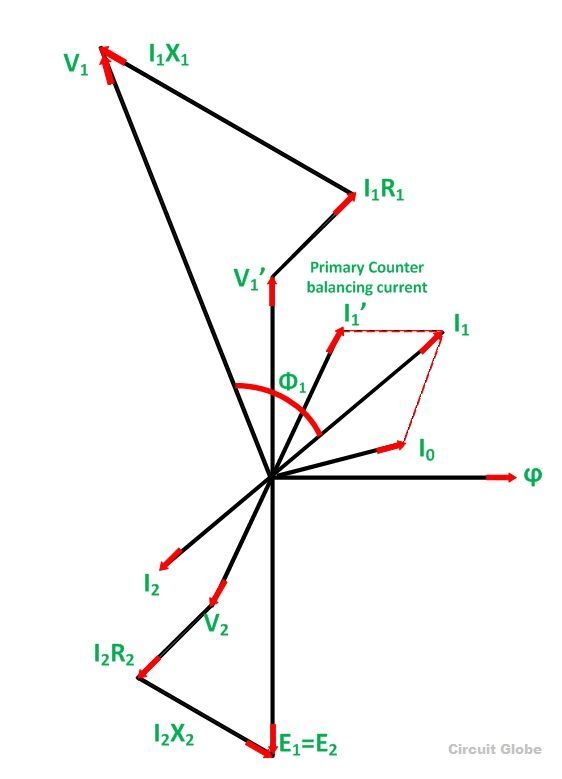
The phasor diagram of the actual transformer when it is loaded inductively is shown below:
Steps to draw the phasor diagram
- Take flux ϕ, a reference
- Induces emf E1 and E2 lags the flux by 90 degrees.
- The component of the applied voltage to the primary equal and opposite to induced emf in the primary winding. E1 is represented by V1’.
- Current I0 lags the voltage V1’ by 90 degrees.
- The power factor of the load is lagging. Therefore current I2 is drawn lagging E2 by an angle ϕ2.
- The resistance and the leakage reactance of the windings result in a voltage drop, and hence secondary terminal voltage V2 is the phase difference of E2 and voltage drop.
V2 = E2 – voltage drops
I2 R2 is in phase with I2 and I2X2 is in quadrature with I2.
- The total current flowing in the primary winding is the phasor sum of I1’ and I0.
- Primary applied voltage V1 is the phasor sum of V1’ and the voltage drop in the primary winding.
- Current I1’ is drawn equal and opposite to the current I2
V1 = V1’ + voltage drop
I1R1 is in phase with I1 and I1XI is in quadrature with I1.
- The phasor difference between V1 and I1 gives the power factor angle ϕ1 of the primary side of the transformer.
- The power factor of the secondary side depends upon the type of load connected to the transformer.
- If the load is inductive as shown in the above phasor diagram, the power factor will be lagging, and if the load is capacitive, the power factor will be leading. Where I1R1 is the resistive drop in the primary windings
I2X2 is the reactive drop in the secondary winding
Similarly
Phasor Diagram of Transformer on Capacitive Load
The Transformer on the Capacitive load (leading power factor load) is shown below in the phasor diagram.

Steps to draw the phasor diagram at capacitive load
- Take flux ϕ a reference
- Induces emf E1 and E2 lags the flux by 90 degrees.
- The component of the applied voltage to the primary equal and opposite to induced emf in the primary winding. E1 is represented by V1’.
- Current I0 lags the voltage V1’ by 90 degrees.
- The power factor of the load is leading. Therefore current I2 is drawn leading E2
- The resistance and the leakage reactance of the windings result in a voltage drop, and hence secondary terminal voltage V2 is the phasor difference of E2 and voltage drop.
V2 = E2 – voltage drops
I2 R2 is in phase with I2 and I2X2 is in quadrature with I2.
- Current I1’ is drawn equal and opposite to the current I2
- The total current I1 flowing in the primary winding is the phasor sum of I1’ and I0.
- Primary applied voltage V1 is the phasor sum of V1’ and the voltage drop in the primary winding.
V1 = V1’ + voltage drop
I1R1 is in phase with I1 and I1XI is in quadrature with I1.
- The phasor difference between V1 and I1 gives the power factor angle ϕ1 of the primary side of the transformer.
- The power factor of the secondary side depends upon the type of load connected to the transformer.
This is all about the phasor diagram on various loads.

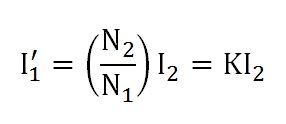
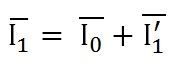
Very good explained.. Clear all doubts, thanks..
It’s really helpful
I like it
Thanks very nice notes and very helpful
very well explained.
helped a lot.
thanks..
Thanks
Great Content.
It is very easy process
And it is very well
I have doubt why voltage drop due to resistance is in phase with current
Ohm’s Law
Thank you, this is very well explained. I however have some clarifications i would like to request for..
Current I0 lags the voltage V1’ by 90 degrees. <- is this correct or is it V1
Current I1’ is drawn equal and opposite to the current I2 <- is this correct or is it I1
thanks!! 🙂
Very very nicely explained . Thanks so much
I think it is the best explained topic ever,being searched in google
helped me so much,
thanks