The Two Wattmeter Method is explained, taking an example of a balanced load. In this, we have to prove that the power measured by the two wattmeter i.e. the sum of the two wattmeter readings is equal to root 3 times of the phase voltage and line voltage (√3VLIL Cosϕ) which is the actual power consumed in a 3 phase balanced load.
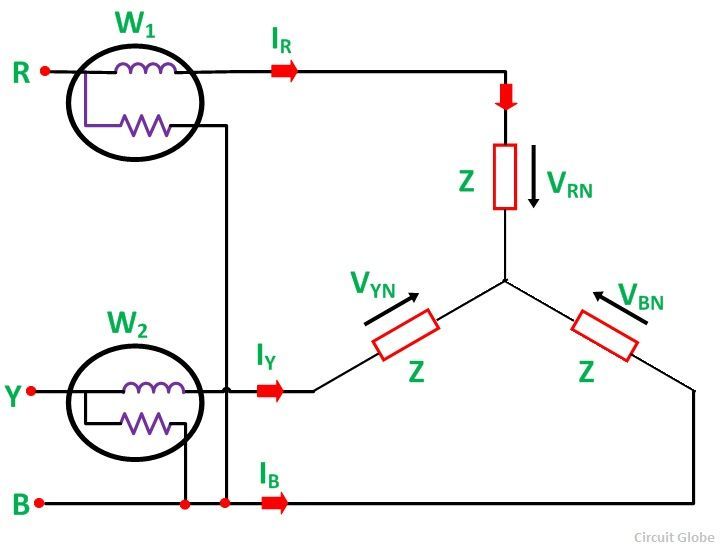
The connection diagram of a 3 phase balanced load connected as Star Connection is shown below:
Contents:
- Determination of Power Factor from Wattmeter Readings
- Determination of Reactive Power by Two Wattmeter Method
The load is considered as an inductive load, and thus, the phasor diagram of the inductive load is drawn below:
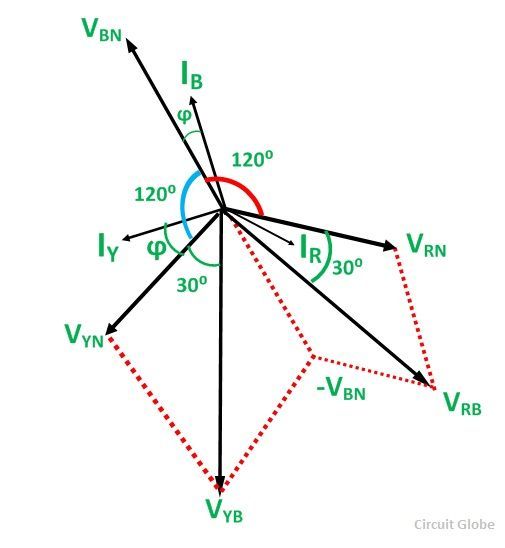 The three voltages VRN, VYN and VBN, are displaced by an angle of 120 degrees electrical as shown in the phasor diagram. The phase current lag behind their respective phase voltages by an angle ϕ.
The three voltages VRN, VYN and VBN, are displaced by an angle of 120 degrees electrical as shown in the phasor diagram. The phase current lag behind their respective phase voltages by an angle ϕ.
Now, the current flowing through the current coil of the wattmeter, W1 will be given as:
The potential difference across the pressure or potential coil of the wattmeter, W1 will be:
To obtain the value of VYB, reverse the phasor VBN and add it to the phasor VYN as shown in the phasor diagram above.
The phase difference between VRB and IR is (30⁰ – ϕ)
Therefore, the power measured by the Wattmeter, W1 is:
Current through the current coil of the Wattmeter, W2 is given as:
The potential difference across the Wattmeter, W2 is
The phase difference VYB and IY is (30⁰ + ϕ).
Therefore, the power measured by the wattmeter, W2 is given by the equation shown below:
Since, the load is in a balanced condition, hence,
Therefore, the wattmeter readings will be:
Now, the sum of two Wattmeter readings will be given as:
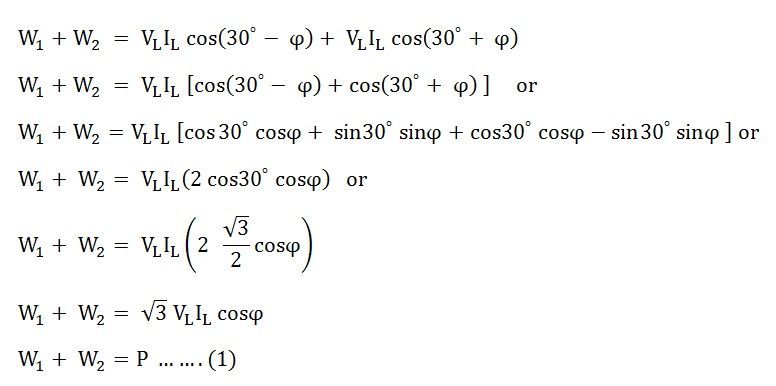 The above equation (1) gives the total power absorbed by a 3 phase balanced load.
The above equation (1) gives the total power absorbed by a 3 phase balanced load.
Thus, the sum of the readings of the two Wattmeters is equal to the power absorbed in a 3 phase balanced load.
Determination of Power Factor from Wattmeter Readings
As we know,
Now,
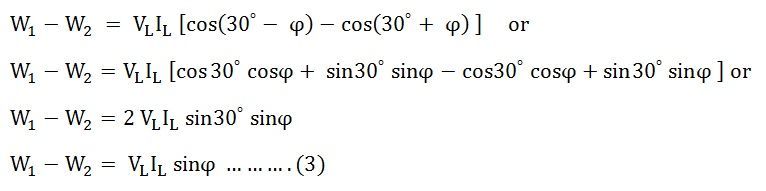 Dividing equation (3) by equation (2) we get,
Dividing equation (3) by equation (2) we get,
The power factor of the load is given as
Determination of Reactive Power by Two Wattmeter Method
To get the reactive power, multiply equation (3) by √3.
Therefore, reactive power is given by the equation shown below:
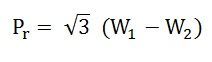 For the Measurement of the three-phase power, you can also refer the two topics given below:
For the Measurement of the three-phase power, you can also refer the two topics given below:
Also See: Measurement of Three-Phase Power: Three Wattmeter Method
Also See: Two Wattmeter Method of Power Measurement.

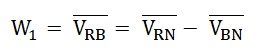
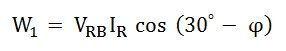
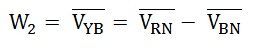
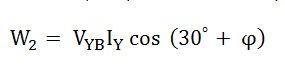
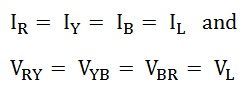
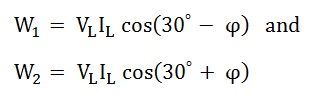

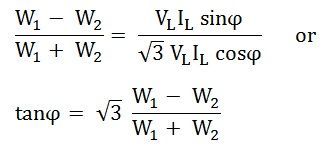
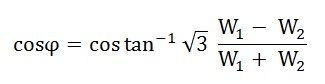
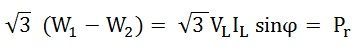
excellent
Great explanation
Was really helpful before my exams. Well written!!!
excellent
Thank you, this is an exceptional explanation.
Useful
helpful
Helpful