Current Division Rule
A parallel circuit acts as a current divider as the current divides in all the branches in a parallel circuit, and the voltage remains the same across them. The current division rule determines the current across the circuit impedance. The current division is explained with the help of the circuit shown below:
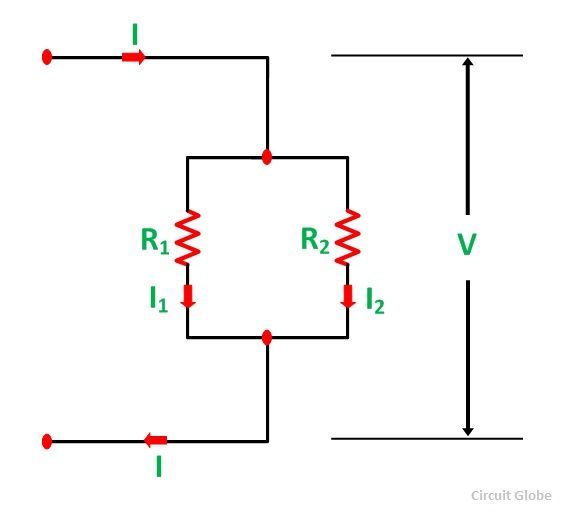 The current I has been divided into I1 and I2 into two parallel branches with the resistance R1 and R2 and V is the voltage drop across the resistance R1 and R2.
The current I has been divided into I1 and I2 into two parallel branches with the resistance R1 and R2 and V is the voltage drop across the resistance R1 and R2.
As we know,
V = IR ……..(1)
Then the equation of the current is written as:
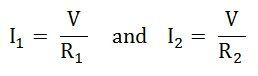
Let the total resistance of the circuit be R and is given by the equation shown below:
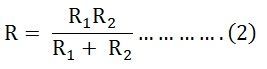
Equation (1) can also be written as:
I = V/R ……….(3)
Now, putting the value of R from the equation (2) in the equation (3) we will get
Putting the value of V = I1R1 from the equation (5) in equation (4), we finally get the equation as:
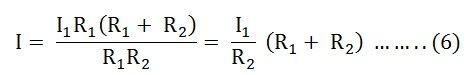
And now considering V = I2R2 the equation will be:
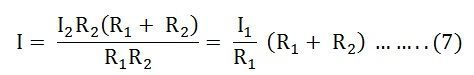
Thus, from the equation (6) and (7) the value of the current I1 and I2 respectively is given by the equation below:
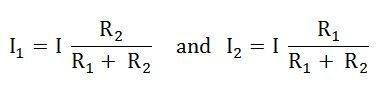
Thus, in the current division rule, it is said that the current in any of the parallel branches is equal to the ratio of opposite branch resistance to the total resistance, multiplied by the total current.
Voltage Division Rule
The voltage division rule can be understood by considering a series circuit shown below. In a series circuit, voltage is divided, whereas the current remains the same.
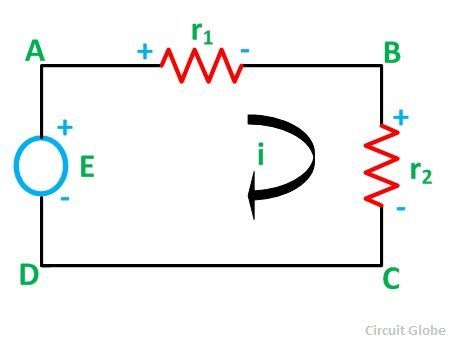 Let us consider a voltage source E with the resistance r1 and r2 connected in series across it.
Let us consider a voltage source E with the resistance r1 and r2 connected in series across it.
As we know,
I = V/R or we can say I = E/R
Therefore, the current (i) in the loop ABCD will be:
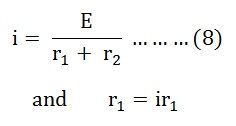
By putting the value of I from equation (8) in equation (9) the voltage across the resistance r1 and r2 respectively are given by the equation shown below as:
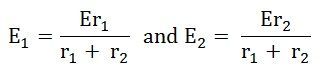
Thus, the voltage across a resistor in a series circuit is equal to the value of that resistor times the total impressed voltage across the series elements divided by the total resistance of the series elements.

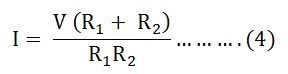
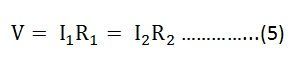
greatly assisted
V.helpful guys…thanks
thank you…
thanks, sir, it helps me a lot.
Help full and well explained
thanks
Thank u helped me to pass exam
well explained