A Direct Current Motor, DC is named according to the connection of the field winding with the armature. Mainly there are two types of DC Motors. One is Separately Excited DC Motor and other is Self-excited DC Motor.
The self-excited motors are further classified as Shunt wound or shunt motor, Series wound or series motor and Compound wound or compound motor.
The dc motor converts electrical power into mechanical power. The construction of the dc motor and generator are the same. But the dc motor has a wide range of speed and good speed regulation in electric traction.
The working principle of the dc motor is based on the principle that the current-carrying conductor is placed in the magnetic field and a mechanical force is experienced by it.
The DC motor is generally used in the location that requires a protective enclosure, for example, drip-proof, the fireproof, etc. according to the requirements. The detailed description of the various types of motor is given below.
Contents:
- Separately Excited DC Motor
- Self Excited DC Motor
- Shunt Wound Motor
- Series Wound Motor
- Compound Wound Motor
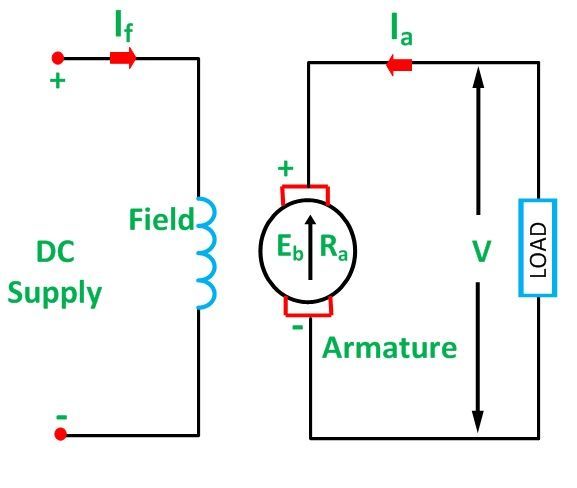
Separately Excited DC Motor
As the name signifies, the field coils or field windings are energised by a separate DC source as shown in the circuit diagram shown below:
Self Excited DC Motor
As the name implies self-excited, hence, in this type of motor, the current in the windings is supplied by the machine or motor itself. Self-excited DC Motor is further divided into shunt wound, and series wound motor. They are explained below in detail.
Shunt Wound Motor
This is the most common types of DC Motor. Here the field winding is connected in parallel with the armature as shown in the figure below:
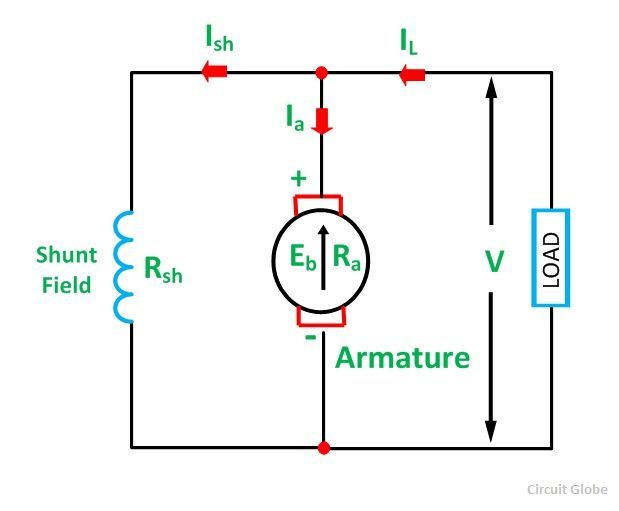
The current, voltage and power equations for a shunt motor are written as follows.
By applying KCL at junction A in the above figure.
The sum of the incoming currents at A = Sum of the outgoing currents at A.
Where,
I is the input line current
Ia is the armature current
Ish is the shunt field current
Equation (1) is the current equation.
The voltage equations are written by using Kirchhoff’s voltage law (KVL) for the field winding circuit.
For armature winding circuit the equation will be given as:
The power equation is given as:
Power input = mechanical power developed + losses in the armature + loss in the field.
Multiplying equation (3) by Ia we get the following equations.
Where,
VIa is the electrical power supplied to the armature of the motor.
Series Wound Motor
In the series motor, the field winding is connected in series with the armature winding. The connection diagram is shown below:
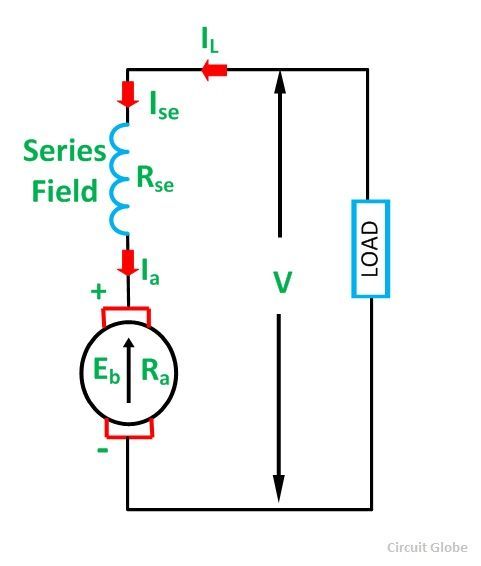
By applying the KCL in the above figure:
Where,
Ise is the series field current
The voltage equation can be obtained by applying KVL in the above figure.
The power equation is obtained by multiplying equation (8) by I we get
Power input = mechanical power developed + losses in the armature + losses in the field
Comparing the equation (9) and (10), we will get the equation shown below:
Compound Wound Motor
A DC Motor having both shunt and series field windings is called a Compound Motor. The connection diagram of the compound motor is shown below:
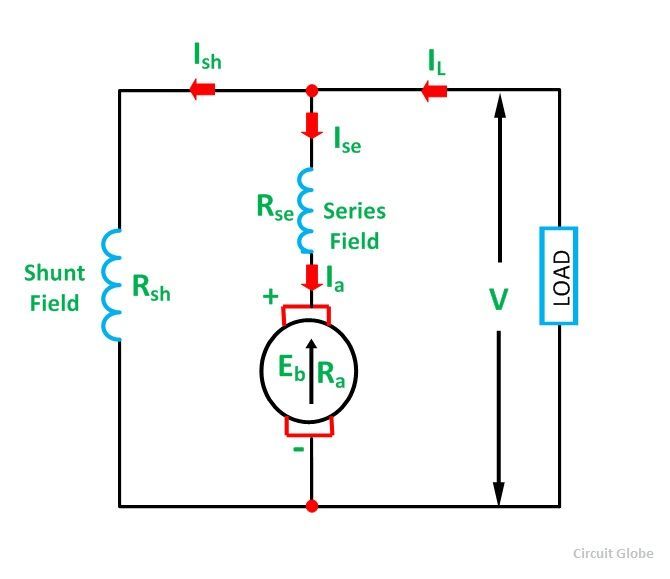
The compound motor is further subdivided as Cumulative Compound Motor and Differential Compound Motor. In a cumulative compound motor the flux produced by both the windings is in the same direction, i.e.
In differential compound motor, the flux produced by the series field windings is opposite to the flux produced by the shunt field winding, i.e.
The positive and negative sign indicates that the direction of the flux produced in the field windings.

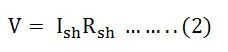
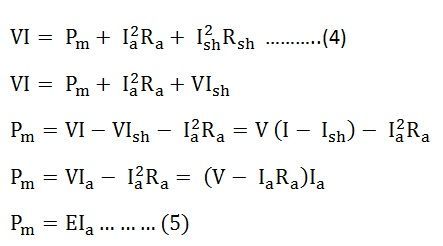
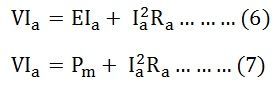
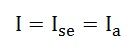
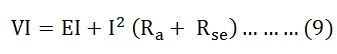
You left out the long-shunt and short shunt compound motor connection. I took a class in motors and generators last year and the instructor indicated that there is a difference in the performance of long shunt and short shunt motors and generators, and one is more suited to each application, but I can’t remember which.
thank you so much for your contribution!
All the informations are very clearly explained in all the pages… Tq so much
All the work is clearly explained. Thanks so much!
nice explanation .thank you so much
Thank you for such easy explanation through diagrams. I have clearly understood the equations as well.
nice explanation
Simplified and easy to understand. Thanks
Very nicely explained. Thank you
Nice
Thank you