The Nodal Voltage Analysis is a method to solve the electrical network. It is used where it is essential to compute all branch currents.The nodal voltage analysis method determines the voltage and current by using the nodes of the circuit.
A node is a terminal or connection of more than two elements. The nodal voltage analysis is commonly used for networks having many parallel circuits with a common terminal ground.
This method requires less number of the equation for solving the circuit.
In Nodal Voltage Analysis, Kirchhoff’s Current Law (KCL) is used, which states that the algebraic sum of all incoming currents at a node must be equal to the algebraic sum of all outgoing currents at that node.
It is the method of finding the potential difference between the elements or branches in an electric circuit. This method defines the voltage at each node of the circuit. This method has two types of nodes. These are the non-reference node and the reference node.
The non-reference nodes have a fixed voltage, and the reference node is the reference points for all other nodes.
In the nodal method, the number of independent node pair equations needed is one less than the number of junctions in the network. That is if n denotes the number of independent node equations and j is the number of junctions.
n = j – 1
In writing the current expression, the assumptions are made that the node potentials are always higher than the other voltages appearing in the equations.
Let us understand the Nodal Voltage Analysis Method with the help of an example shown below:
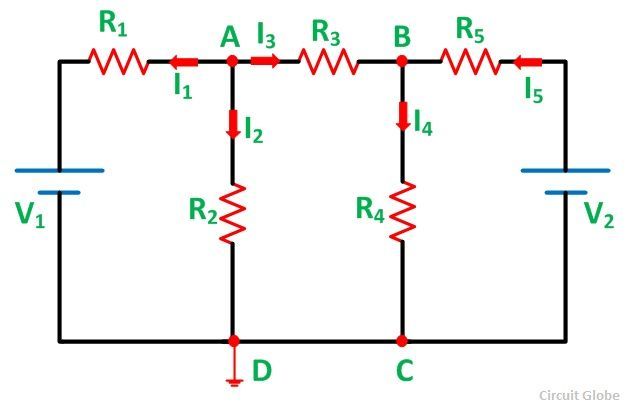 Steps for Solving Network by Nodal Voltage Analysis Method
Steps for Solving Network by Nodal Voltage Analysis Method
Considering the above circuit diagram, the following steps are explained below
Step 1 – Identify various nodes in the given circuit and mark them
in the given circuit, we have marked the nodes as A and B.
Step 2 – Select one of the nodes as the reference or zero potential nodes at which a maximum number of elements are connected, is taken as reference.
In the above figure, node D is taken as the reference node. Let the voltages at nodes A and B be VA and VB respectively.
Step 3 – Now apply KCL at the different nodes.
Applying KCL at node A, we have
Where,
Applying KCL at the node B, we have
Solving equation (1) and the equation (2) we will get the value of VA and VB.
The nodal voltage analysis has the advantage that a minimum number of equations needs to be written to determine the unknown quantities.

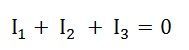
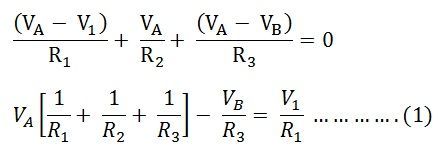
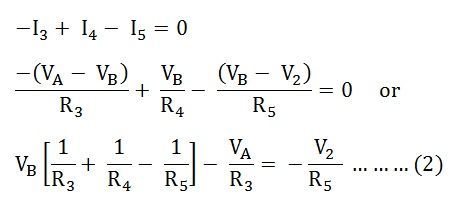
nice information here