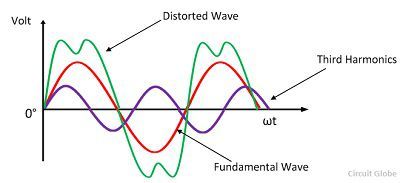
The harmonic is the distortion in the waveform of the voltage and current. It is the integral multiple of some reference waves. The harmonic wave increases the core and copper loss of the transformer and hence reduces their efficiency. It also increases the dielectric stress on the insulation of the transformer.
In a three-phase transformer, the non-sinusoidal nature of magnetising current produces sinusoidal flux which gives rise to the undesirable phenomenon. The phase magnetising currents in transformer should contain third harmonics and higher harmonics necessary to produce a sinusoidal flux.
If the phase voltage across each phase is to remain sinusoidal, then the phase magnetising currents must be of the following form.
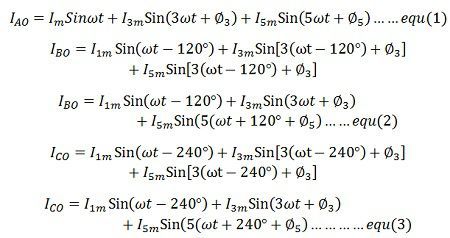It is seen from equation (1), (2), and (3) that the third harmonics in the three currents are co-phase, that is they have the same phase. The fifth harmonics have different phases.
Delta Connection
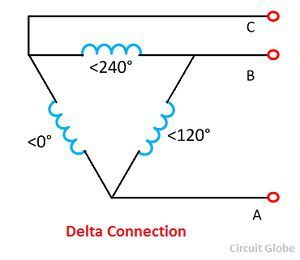Let the IAO, IBO and the ICO represent the phase magnetising current in a delta connection. The line currents can be found by subtracting two phases current. For examples,
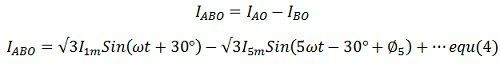The third harmonic present in the phase magnetising current of three phase transformer is not present in the line current. The third harmonic components are co-phase and hence cancel out in the line. The third harmonic components are flows rounds the closed loop of the delta.
The delta connection only allows a sinusoidal flux and voltage with no third harmonic current in the transmission line. For this reason majority of the 3-phase transformer has delta connected windings and in places where it is not convenient to have an either primary or secondary connected in delta, a tertiary winding is provided. The tertiary windings carry the circulating third harmonics current required by the sinusoidal flux in each limb of the core.
In a delta connection, the voltage acting around the closed delta is,
This is a third harmonic voltage and it will circulate a third harmonic current round the closed loop of the delta
Star connection
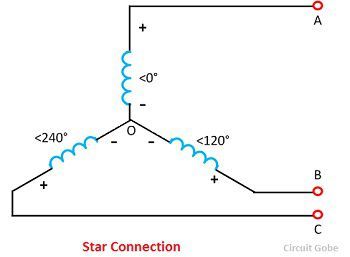If IAO, IBO and ICO, represents the phase magnetising current in a star connection,
Where In is the current in the neutral wire.
The harmonics above the seventh be neglected. The equation (6) shows that under the balanced condition the current flow in the neutral wire is the third harmonic current. The magnitude of the third harmonics current is thrice the magnitude of each third phase current. The thirds harmonic current produced inductive interference with communication circuit. If the supply to the star connection is three wires, neutral current must be zero and therefore
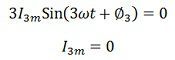Thus, it is seen that the three wire star connection suppresses the flow of harmonic and magnetising currents. For a four wire star-connected system, the in phase third harmonic current flow in the neutral wire.
Similarly, the third balance phase voltage containing harmonics can be written as
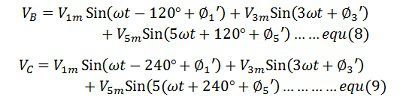The equation (7), (8) and (9) shows that the third harmonics in the three phase voltage have the same phase. The line voltage in a star connection can be obtained by subtracting two phase voltages. For example
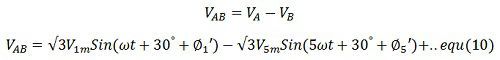From equation (10) it is seen that the third harmonics is not present in the line to line voltage of a star connection. This applies to all triplers harmonics.
very good understanding of the third harmonic. thank you