Space harmonics fluxes are produced by the windings, slotting, magnetic saturation, inequalities in the air gap length. These harmonic fluxes induce voltages and circulate harmonic currents in the rotor windings. The interaction between the harmonic currents generated in the rotor and the harmonic fluxes results in the Harmonic torques, vibrations, and the noise.
The air gap flux set up by the three-phase stator windings carrying sinusoidal currents. The wave shape is non-sinusoidal in nature. According to Fourier series analysis, any non-sinusoidal flux is equivalent to the combination of a number of sinusoidal fluxes of fundamental and higher-order harmonics. Since the flux wave shape has half-wave symmetry, all even harmonics (2,4,6 ……) are absent in the Fourier series.
A non-sinusoidal flux can be resolved into fluxes of fundamental and higher-order odd harmonics (3, 5, 7, 11, 13, etc). The third harmonic flux wave produced by each of the three phases neutralizes one another. The resultant air-gap flux is free from third harmonics and its multiples. This is because the third harmonics in the flux wave of all the three phases are in the space phase, but differ in the time phase by 120 degrees.
Harmonics Induction Torques
A 3 phase winding carrying a sinusoidal current produces space harmonics of the order h = 6k ± 1, where k is a positive integer (1, 2, 3…..). The synchronous speed of the hth harmonic is (1/h) times the speed of the fundamental wave. Space harmonic waves rotate in the same direction as the fundamental wave, if h = 6k + 1 and if h = 6k – 1 then it rotates in the opposite direction.
Space harmonic wave of the order h, is equivalent to a machine with the number of poles equal to (h x number of poles of the stator). Therefore, the synchronous speed of the hth space harmonic wave is: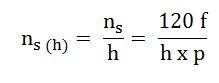
Where,
- f = supply frequency
- P = number of poles of the stator
Thus, for the value of k = 1, a 3 phase winding will produce a backward rotating fifth harmonic at the speed of (1/5) of the synchronous speed and forward rotating seventh harmonic rotating at a speed of (1/7) of the synchronous speed. These harmonics alone will have an effect on the operation of the motor.
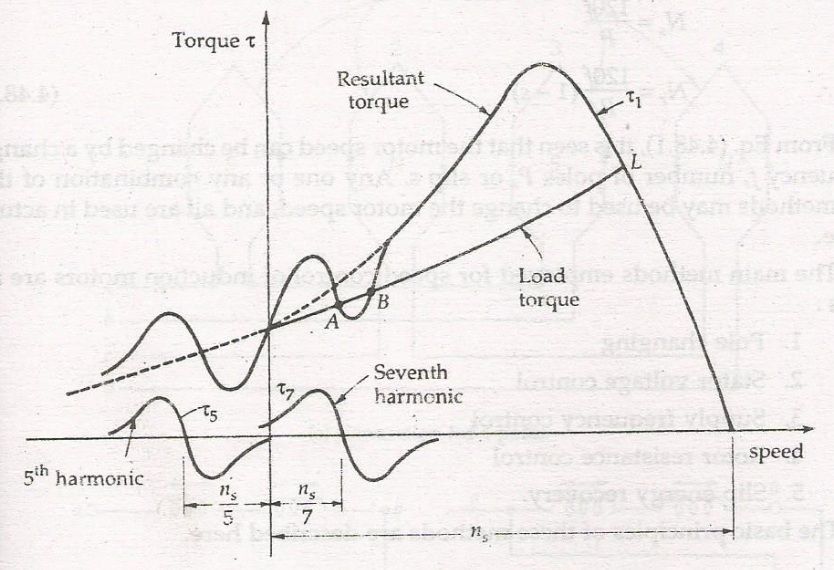
The speed-torque characteristics of the fundamental flux and the fifth and seventh space harmonic flux are shown below:
The fifth harmonic torque opposes the fundamental component torque as the fifth harmonic flux rotates in the opposite to the rotation of the rotor. Thus, the fifth harmonic flux produces a braking torque. The seventh harmonic flux rotates in the same direction as that of the fundamental flux. Hence, the resultant torque-speed characteristic will be the combination of the fundamental fifth and seventh harmonic characteristics.
The resultant torque-speed characteristics have two dips, one near (1/5) of the synchronous speed and the other near (1/7) of the synchronous speed. The dip near (1/5) of the synchronous speed occurs in the negative direction of the motor rotation.
The motor will accelerate to point L, which is the interaction between the load torque characteristic and the motor torque-speed curve. This motor torque is developed because of the fundamental flux alone. The load torque curve intersects the motor torque-speed characteristics at point A, this is because of the presence of the seventh harmonics flux torque. The seventh harmonic flux torque curve has a negative slope at point A.
The motor torque falls below the load torque. At this stage, the motor will not accelerate up to its normal speed but will remain running at a speed that is nearly (1/7) of its normal speed, and the operating point is A. This tendency of the motor to run at a stable speed as low as one-seventh of the normal speed Ns. In this condition the motor is unable to pick up its normal speed is known as crawling of the motor.
Crawling can be reduced by reducing fifth and seventh harmonics. This can be done by using a chorded or short pitched winding.

Honestly it’s the best explanation I have found so far
Best Explanation
very nice explanation
all the questions of my booklet have been solved after learning from these notes. Thanks
Very helpful study material for engineering student