Definition: The economic load dispatch means the real and reactive power of the generator vary within the certain limits and fulfils the load demand with less fuel cost. The sizes of the electric power system are increasing rapidly to meet the energy requirement. So the number of power plants is connected in parallel to supply the system load by an interconnection of the power system. In the grid system, it becomes necessary to operate the plant units more economically.
The economic scheduling of the generators aims to guarantee at all time the optimum combination of the generator connected to the system to supply the load demand.The economic load dispatch problem involves two separate steps. These are the online load dispatch and the unit commitment.
The unit commitment selects that unit which will anticipate load of the system over the required period at minimum cost. The online load dispatch distributes the load among the generating unit which is parallel to the system in such a manner as to reduce the total cost of supplying. It also fulfils the minute to the minute requirement of the system.
Basic Mathematical Formulation
Consider n generators in the same plant or close enough electrically so that the line losses may be neglected. Let C1, C2, …, Cn be the operating costs of individual units for the corresponding power outputs P1, P2,…., Pn respectively. If C is the total operating cost of the entire system and PR is the total power received by the plant bus and transferred to the load, then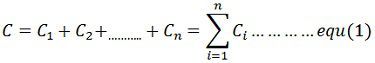
 The equation (1) and equation (2) can be minimised as
The equation (1) and equation (2) can be minimised as
The above equation shows that if transmission losses are neglected, the total demand PR at any instant must be met by the total generation. The above equation is the equality constraint.
This a constrained minimising problem. This problem can be solved by using Lagrangian multiplier technique.
where f is the equality constraint equation given by
And λ is the Lagrange multiplier. Combination of equations (3) and (4) gives
Equation (5) can be solved for minimum by determining the partial derivate of the function C* on variable Pi and equating it equal to zero.
Since Ci is a function of Pi only. The partial derivates become full derivates, that is,
Therefore, the condition for optimum operation is
Since the dci / dpi is the increment cost generation for the generator. The above equation shows that the criterion for a most economical division of load between within a plant is that all the unit is must operate at the same incremental fuel cost. This is known as the principle of equal λ criterion or the equal incremental cost-loading principle for economic operation.

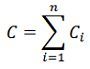
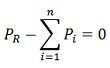
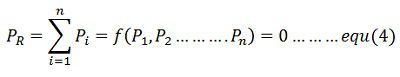

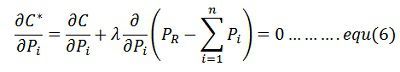
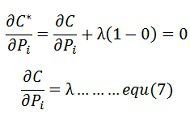
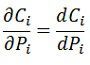
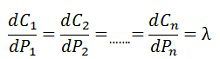
Excellent…….
thanks