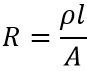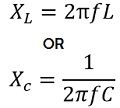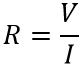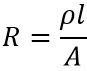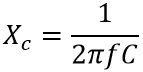Resistance and Reactance are the two major terms that combinedly form impedance of an electrical circuit. The crucial difference between resistance and reactance is that resistance is the hindrance to the flow of electric current by only resistor. As against reactance is the opposition to the change in current by either inductor or capacitor.
Basically, the obstruction to the flow of electrical current in any circuit is defined as impedance. Impedance is a complex term and is a combination of real and imaginary values. In this section, we will discuss the various differentiating factors between resistance and reactance using the comparison chart.
Content: Resistance Vs Reactance
Comparison Chart
| Parameter | Resistance | Reactance |
|---|---|---|
| Basic | It is the obstruction by resistor to the flow of current. | It is the opposition to the varying current in a circuit by inductor or capacitor. |
| Symbolic representation |  |  |
| Denoted by | R | X |
| Given by |  |  |
| Type of circuit | Both AC and DC circuit. | Specifically AC circuit. |
| Circuit element | Pure resistor | Ideal inductor or capacitor. |
| Nature of value | Real part of impedance. | Imaginary part of impedance. |
| Depends on | Dimensions, resistivity and temperature of conductor. | Frequency of alternating current. |
| Phase difference between V and I | V and I are in same phase. Thus phase difference is 0 degree. | There exist a phase difference of 90 degrees between V and I. |
| Electric power | The overall power gets dissipated in the form of heat. | A part of supplied power gets stored. |
Definition of Resistance
The obstruction in the path of current flowing through the circuit is known as resistance. We know when a certain potential is applied to an electrical circuit then current in proportion to the applied voltage flows through the circuit. However, a certain amount of hindrance also exists in the path of the flowing current. This property of opposing the flowing current is known as resistance.
Resistance is the property possessed by resistors in electrical circuits. So, in other words, we can say that the ratio of supplied voltage and flowing current in an electric circuit having resistor as the load is known as resistance. Thus the resistance of the circuit is given as:
The resistance of any electrical circuit is measured in ohms and it shows dependency with resistivity and dimensions of the respective conductors. Thus offered resistance is specified as:
It is to be noted here that resistance offered by the conductors is the same for constant or varying current. In resistive circuits, the power consumed is given as:
As both the terms in the product are real values thus the consumed power will also be a real term. Thereby indicating that the supplied power gets fully utilized in the resistive circuit.
Definition of Reactance
The obstruction to the flow of alternating or changing current in electric circuits is known as reactance. The reactance to the circuit is the opposition in the flow of varying current.
The reason behind the reactance of the circuit is such that its value is the factor of the presence of either capacitor or inductor as load. So, it can be said in a way that the ratio of the voltage applied and the changing current in an electric circuit with the load as either capacitive or inductive is known as reactance of that circuit.
For inductive load the reactance is given as:
In the case of capacitive load, the reactance is given as:
Therefore, reactance is said to be directly proportional to frequency in the case of the inductive circuit. While it is inversely proportional to the capacitive circuit.
Whenever alternating current flows through a circuit with the inductive or capacitive load then changing energy is stored in either an electric field or magnetic field. In the case of the inductive load, there is a changing magnetic field. While for capacitive load there is an electric field.
As we have already discussed that resistance and reactance conjugately forms a complex value termed impedance, where the reactance acts as the imaginary part of the complex value. Inductive reactance is generally a positive imaginary value thus with the increase in inductive load, the reactance offered by it also increases.
Key Differences Between Resistance and Reactance
- The resistance is the obstacle in the flow of current in an electrical circuit due to resistor. While reactance is the opposition to the charging current due to either inductor or capacitor.
- Resistance is the property associated with both ac and dc circuit. However, reactance to the property is only associated with ac circuits.
- Pure resistors generate resistance. As against ideal inductors or capacitors give rise to reactance in the circuit.
- Resistance is associated with the real part of the impedance. While reactance contributes to the imaginary part of the impedance value.
- The difference in phase between voltage and current in a purely resistive circuit is 0⁰. While the phase difference between voltage and current in an ideal capacitive or inductive circuit is 90⁰. In the case of inductive load, the current lags behind the voltage by 90⁰, and for purely capacitive load voltage lags the current by 90⁰.
- The resistance offered by the circuit depends on the dimension, resistivity, and temperature conditions of the conductor. However, the reactance relies on the frequency component of the alternating current in the circuit. It shows proportionality with frequency in the case of inductive load, whereas this relation is inverse in the case of capacitive load.
- In the resistive circuit, the overall supplied power to the circuit gets dissipated in the form of heat. Whereas in a capacitive or inductive circuit, the device does not fully consume the total supplied power.
Conclusion
So, from this discussion, it can be concluded that both resistance and reactance are responsible for the opposition to the flow of current and thus acts as impedance for any electrical circuit when present combinedly in it.