Maximum Power Transfer Theorem states that – A resistive load, being connected to a DC network, receives maximum power when the load resistance is equal to the internal resistance known as (Thevenin’s equivalent resistance) of the source network as seen from the load terminals. The Maximum Power Transfer theorem is used to find the load resistance for which there would be the maximum amount of power transfer from the source to the load.
The maximum power transfer theorem is applied to both the DC and AC circuit. The only difference is that in the AC circuit the resistance is substituted by the impedance.
The maximum power transfer theorem finds their applications in communication systems which receive low strength signal. It is also used in speaker for transferring the maximum power from an amplifier to the speaker.
Content
- Explanation of Maximum Power Transfer Theorem
- Steps for Solving Network Using Maximum Power Transfer Theorem
Explanation of Maximum Power Transfer Theorem
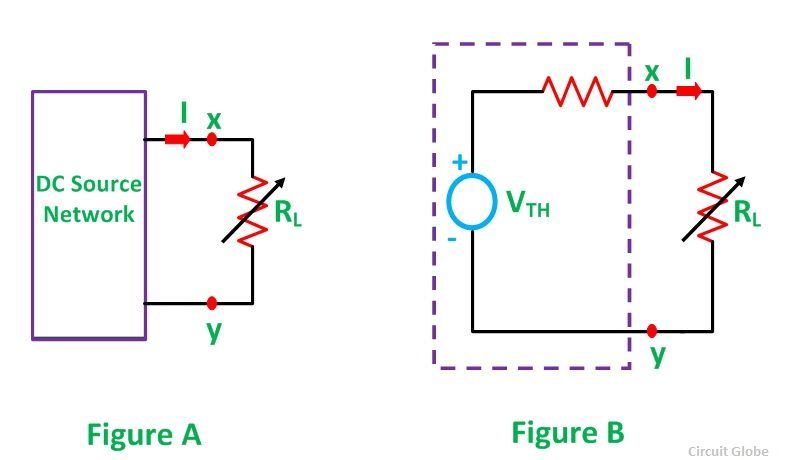
A variable resistance RL is connected to a DC source network as shown in the circuit diagram in figure A below and the figure B represents the Thevenin’s voltage VTH and Thevenin’s resistance RTH of the source network.
The aim of the Maximum Power Transfer theorem is to determine the value of load resistance RL, such that it receives maximum power from the DC source.
 Considering figure B the value of current will be calculated by the equation shown below
Considering figure B the value of current will be calculated by the equation shown below
While the power delivered to the resistive load is given by the equation
Putting the value of I from the equation (1) in the equation (2) we will get
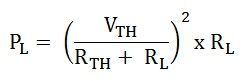
PL can be maximized by varying RL and hence, maximum power can be delivered when (dPL/dRL) = 0
However,
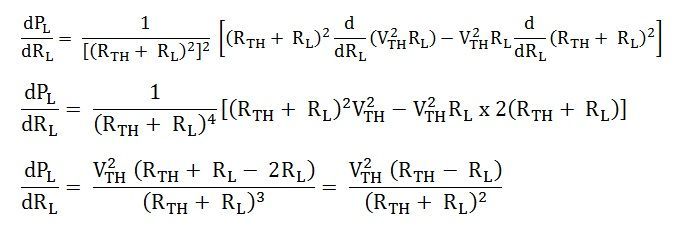 But as we know, (dPL/dRL) = 0
But as we know, (dPL/dRL) = 0
Hence, it is proved that power transfer from a DC source network to a resistive network is maximum when the internal resistance of the DC source network is equal to the load resistance.
Again, with RTH = RL, the system is perfectly matched to the load and the source, thus, the power transfer becomes maximum, and this amount of power Pmax can be obtained by the equation shown below:
Equation (3) gives the power which is consumed by the load. The power transfer by the source will also be the same as the power consumed by the load, i.e. equation (3), as the load power and the source power being the same.
Thus, the total power supplied is given by the equation
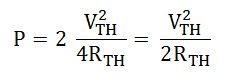
During Maximum Power Transfer the efficiency ƞ becomes:
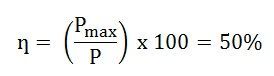
The concept of Maximum Power Transfer theorem is that by making the source resistance equal to the load resistance, which has wide application in communication circuits where the magnitude of power transfer is sufficiently small. To achieve maximum power transfer, the source and the load resistance are matched and with this, efficiency becomes 50% with the flow of maximum power from the source to the load.
In the Electrical Power Transmission system, the load resistance being sufficiently greater than the source resistance, it is difficult to achieve the condition of maximum power transfer.
In power system emphasis is given to keep the voltage drops and the line losses to a minimum value and hence the operation of the power system, operating with bulk power transmission capability, becomes uneconomical if it is operating with only 50% efficiency just for achieving maximum power transfer.
Hence, in the electrical power transmission system, the criterion of maximum power transfer is very rarely used.
Steps for Solving Network Using Maximum Power Transfer Theorem
Following steps are used to solve the problem by Maximum Power Transfer theorem
Step 1 – Remove the load resistance of the circuit.
Step 2 – Find the Thevenin’s resistance (RTH) of the source network looking through the open-circuited load terminals.
Step 3 – As per the maximum power transfer theorem, this RTH is the load resistance of the network, i.e., RL = RTH that allows maximum power transfer.
Step 4 – Maximum Power Transfer is calculated by the equation shown below
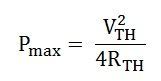
This is all about Maximum Power Transfer Theorem.

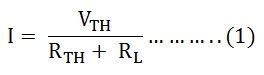
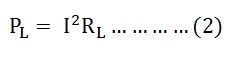
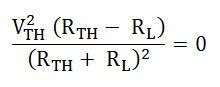

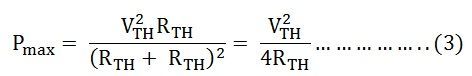
pleaseeeee give also MAX POWER TRANSFER THEOREM FOR AC circuit😁😁😁
why dp/drL=0?…please answer….