Compensation Theorem states that in a linear time-invariant network when the resistance (R) of an uncoupled branch, carrying a current (I), is changed by (ΔR), then the currents in all the branches would change and can be obtained by assuming that an ideal voltage source of (VC) has been connected such that VC = I (ΔR) in series with (R + ΔR) when all other sources in the network are replaced by their internal resistances.
In Compensation Theorem, the source voltage (VC) opposes the original current. In simple words, compensation theorem can be stated as – the resistance of any network can be replaced by a voltage source, having the same voltage as the voltage drop across the resistance which is replaced.
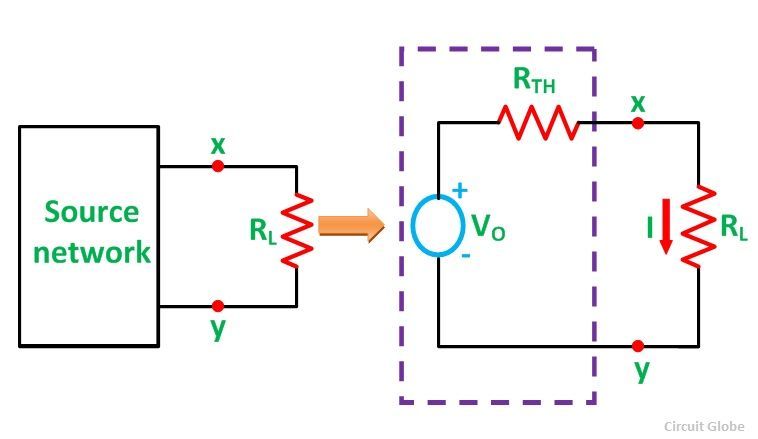
Let us assume a load RL be connected to a DC source network whose Thevenin’s equivalent gives V0 as the Thevenin’s voltage and RTH as the Thevenin’s resistance as shown in the figure below:
Let the load resistance RL be changed to (RL + ΔRL). Since the rest of the circuit remains unchanged, the Thevenin’s equivalent network remains the same as shown in the circuit diagram below:
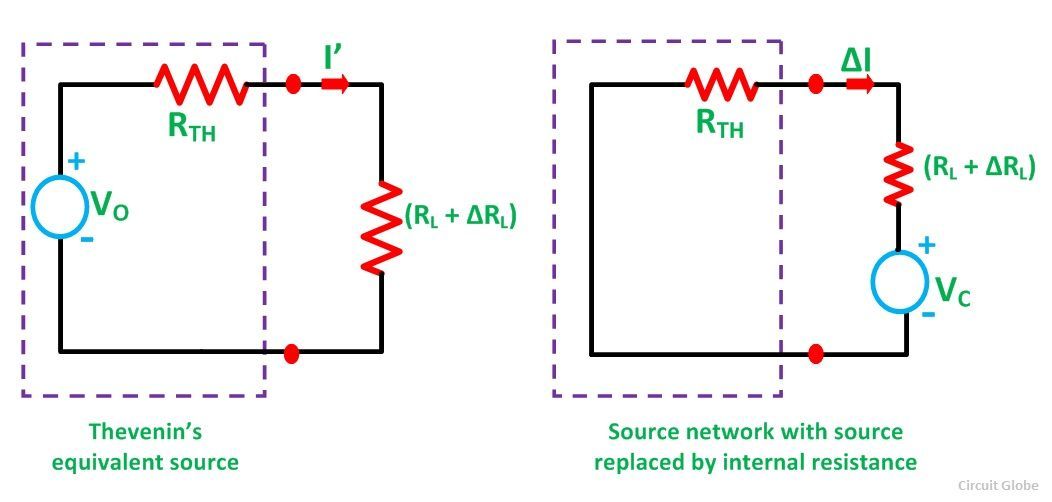 Here,
Here,
The change of current being termed as ΔI
Putting the value of I’ and I from the equation (1) and (2) in the equation (3) we will get the following equation:

Now, putting the value of I from the equation (1) in equation (4), we will get the following equation:
As we know, VC = I ΔRL and is known as compensating voltage.
Therefore, equation (5) becomes,
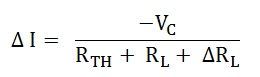
Hence, Compensation theorem tells that with the change of branch resistance, branch currents changes and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current, where all other sources in the network being replaced by their internal resistances.

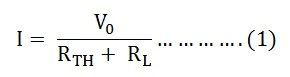
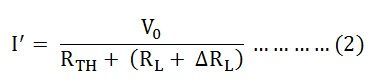
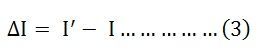
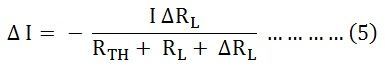
Much useful. Thank you so much