Two Reaction Theory was proposed by Andre Blondel. The theory proposes to resolve the given armature MMFs into two mutually perpendicular components, with one located along the axis of the rotor of the salient pole. It is known as the direct axis or d axis component. The other component is located perpendicular to the axis of the rotor salient pole. It is known as the quadrature axis or q axis component.
The d axis component of the armature MMF, Fa is denoted by Fd, and the q axis component by Fq. The component Fd is either magnetizing or demagnetizing. The component Fq results in a cross-magnetizing effect. If Ψ is the angle between the armature current Ia and the excitation voltage Ef and Fa is the amplitude of the armature MMF, then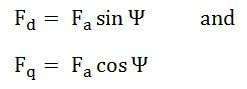
Salient Pole Synchronous Machine Two Rection Theory
In the cylindrical rotor synchronous machine, the air gap is uniform. The pole structure of the rotor of a salient pole machine makes the air gap highly non-uniform. Consider a 2 pole, salient pole rotor rotating in the anticlockwise direction within a 2 pole stator as shown in the figure below:
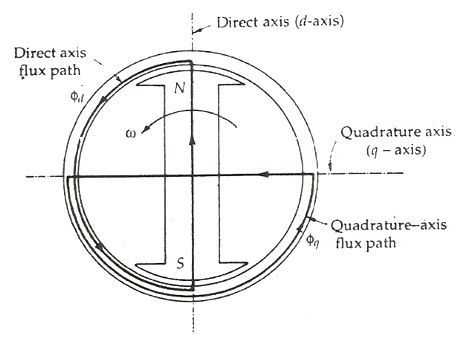 The axis along the axis of the rotor is called the direct or the d axis. The axis perpendicular to the d axis is known as the quadrature or q axis. The direct axis flux path involves two small air gaps and is the path of the minimum reluctance. The path shown in the above figure by ϕq has two large air gaps and is the path of the maximum reluctance.
The axis along the axis of the rotor is called the direct or the d axis. The axis perpendicular to the d axis is known as the quadrature or q axis. The direct axis flux path involves two small air gaps and is the path of the minimum reluctance. The path shown in the above figure by ϕq has two large air gaps and is the path of the maximum reluctance.
The rotor flux BR is shown vertically upwards as shown in the figure below:
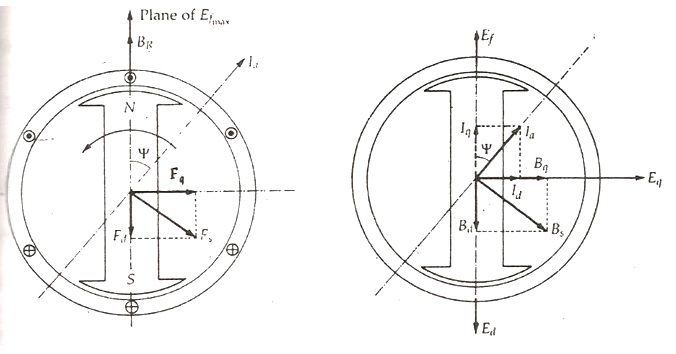 The rotor flux induces a voltage Ef in the stator. The stator armature current Ia will flow through the synchronous motor when a lagging power factor load is connected to it. This stator armature current Ia lags behind the generated voltage Ef by an angle Ψ.
The rotor flux induces a voltage Ef in the stator. The stator armature current Ia will flow through the synchronous motor when a lagging power factor load is connected to it. This stator armature current Ia lags behind the generated voltage Ef by an angle Ψ.
The armature current produces stator magnetomotive force Fs. This MMF lags behind Ia by angle 90 degrees. The MMF FS produces stator magnetic field BS long the direction of Fs. The stator MMF is resolved into two components, namely the direct axis component Fd and the quadrature axis component Fq.
If,
- ϕd is the direct axis flux
- Φq is the quadrature axis flux
- Rd is the reluctance of the direct axis flux path
As, Rd < Rq, the direct axis component of MMF Fd produces more flux than the quadrature axis component of the MMF. The fluxes of the direct and quadrature axis produce a voltage in the windings of the stator by armature reaction.
Let,
- Ead be the direct axis component of the armature reaction voltage.
- Eaq be the quadrature axis component of the armature reaction voltage.
Since each armature reaction voltage is directly proportional to its stator current and lags behind by 90 degrees angles. Therefore, armature reaction voltages can be written as shown below: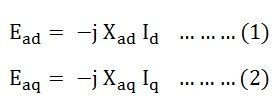
Where,
- Xad is the armature reaction reactance in the direct axis per phase.
- Xaq is the armature reaction reactance in the quadrature axis per phase.
The value of Xad is always greater than Xaq. As the EMF induced by a given MMF acting on the direct axis is smaller than for the quadrature axis due to its higher reluctance.
The total voltage induced in the stator is the sum of EMF induced by the field excitation. The equations are written as follows: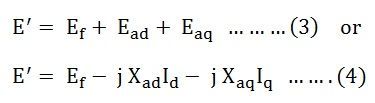
The voltage E’ is equal to the sum of the terminal voltage V and the voltage drops in the resistance and leakage reactance of the armature. The equation is written as: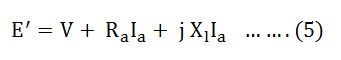
The armature current is divided into two components; one is the phase with the excitation voltage Ef and the other is in phase quadrature to it.
If
- Iq is the axis component of Ia in phase with Ef.
- Id is the d axis Ia lagging Ef by 90 degrees.
Combining the equation (4) and (5) we get,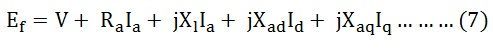
Combining the equation (6) and (7) we get,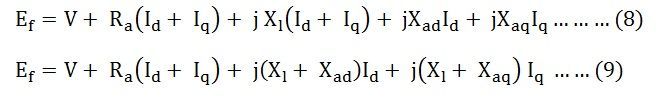 Let,
Let,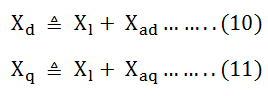
The reactance Xd is called the direct axis synchronous reactance, and the reactance Xq is called the quadrature axis synchronous reactance.
Combining the equations (9) (10) and (11), we get the equations shown below: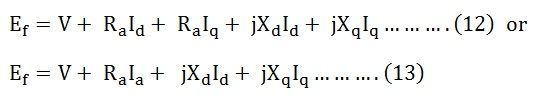 The equation (12) shown above is the final voltage equation for a salient pole synchronous generator.
The equation (12) shown above is the final voltage equation for a salient pole synchronous generator.

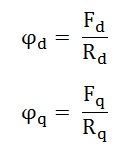
Thanks a lot.
good explanation
good content!!!