Power Flow Diagram of Induction Motor explains the input given to the motor, the losses occurring, and the output of the motor. The input power given to an induction motor is in the form of three-phase voltage and currents. The Power Flow Diagram of an Induction Motor is shown below:
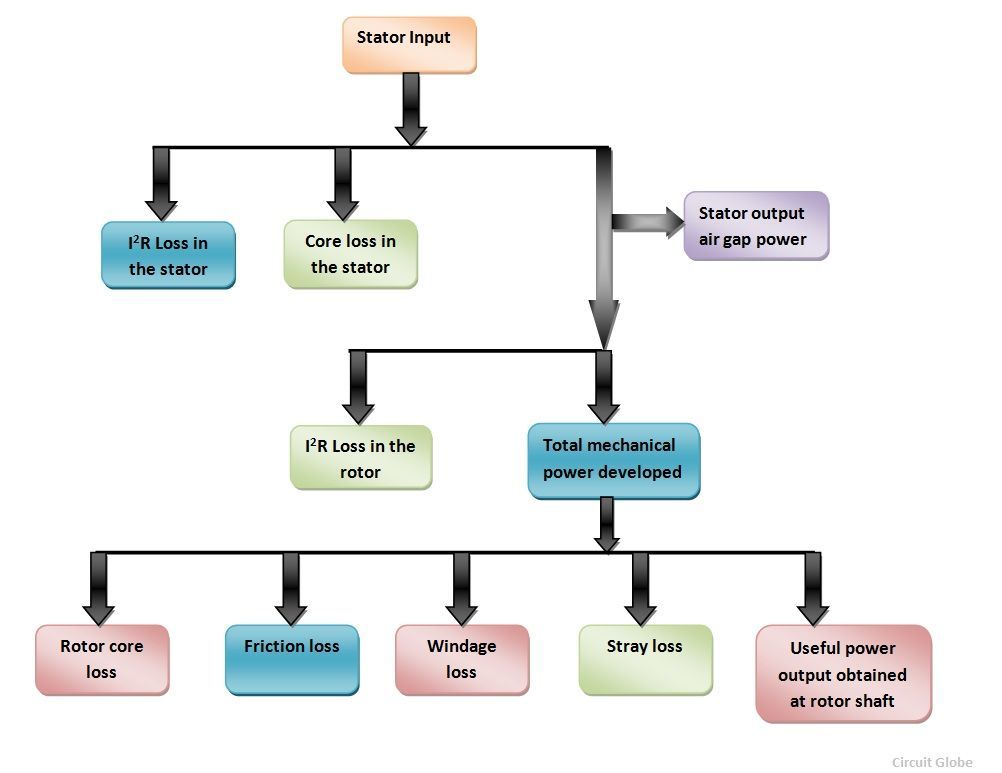 The power flow is given by the equation shown below:
The power flow is given by the equation shown below: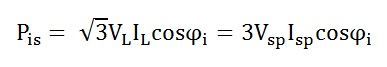
Where cosϕi is the input power factor
The losses in the stator are
I2R losses in the stator winding resistances. It is also known as Stator copper losses.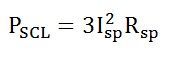
Hysteresis and Eddy current losses in the stator core. These are known as Stator core losses.![]()
The output power of the stator is given as: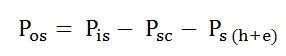
This output power of the stator is transferred to the rotor of the machine across the air gap between the stator and the rotor. It is called the air gap Pg of the machine.
Thus,
Power output of the stator = air gap power = input power to the rotor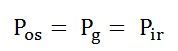
The losses in the rotor are as follows.
I2R losses in the rotor resistance. They are also called Rotor copper losses and represented as: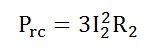
Hysteresis and eddy current losses in the rotor core. They are known as Rotor core losses.![]()
Friction and Windage losses Pfw
Stray load losses Pmisc, consisting of all losses not covered above, such as losses due to harmonic fields.
If the rotor copper losses are subtracted from rotor input power Pg, the remaining power is converted from electrical to mechanical form. This is called Developed Mechanical Power Pmd.
Developed Mechanical power = Rotor input – Rotor copper loss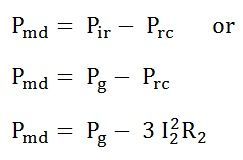
The output of the motor is given by the equation shown below: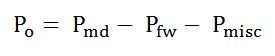
Po is called the shaft power or the useful power.
Rotational losses
At starting and during acceleration, the rotor core losses are high. With the increase in the speed of the induction motor these losses decrease. The friction and windage losses are zero at the start. As the speed increases, the losses also start increasing. The sum of the friction, windage and core losses are almost constant with the change in speed. These all losses are added together and are known as Rotational Losses.
It is given by the equation shown below: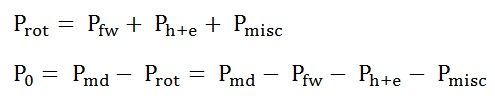
The Rotational losses are not represented by any element of the equivalent circuit as they are purely mechanical quantity.
