Newton Raphson Method is an iterative technique for solving a set of various nonlinear equations with an equal number of unknowns. There are two methods of solutions for the load flow using Newton Raphson Method. The first method uses rectangular coordinates for the variables while the second method uses the polar coordinate form. Out of these two methods the polar coordinate form is used widely.
Let us understand this method with the help of the equations.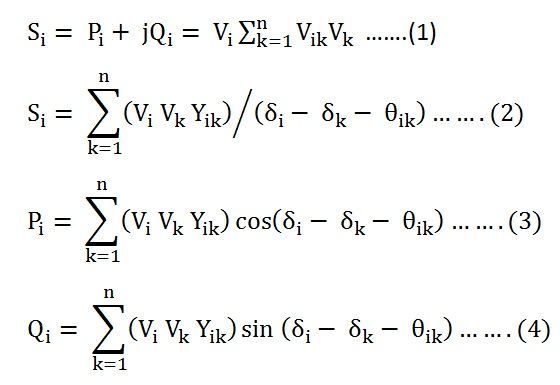
The above equation (3) and (4) can also be written as shown below.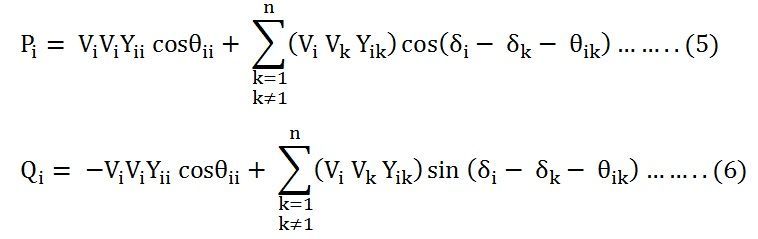
then I = 1, 2, ….n, I ≠ slack, and if
Then I = 1, 2, ….n, i ≠ slack, i ≠ PV bus
Where, the subscripts sp and cal denote the specified and calculated values, respectively, then the equation (7) can be written as shown below.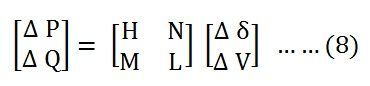
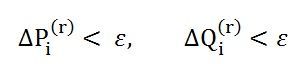
The off diagonal and diagonal elements of the sub matrices H, N, M and L are determined by differentiating equation (3) and (4) with respect to δ and |V|.
Procedure of Newton Raphson Method
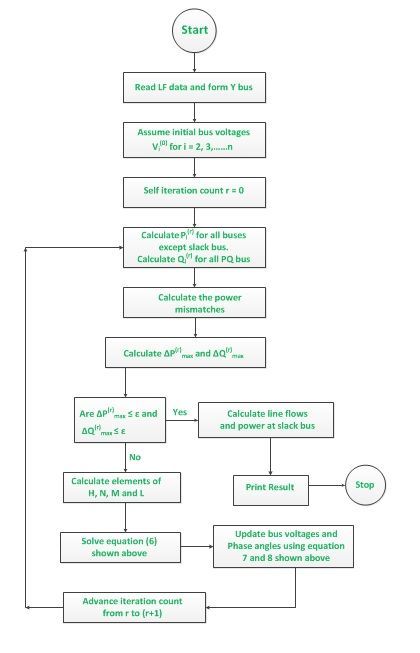
The computational procedure for Newton Raphson Method using polar coordinate is given below.
- Form Y bus.
- Assume the initial value of the bus voltages |Vi|0 and phase angle δi0 for i = 2, 3, …..n for load buses and phase angles for PV buses. Normally we set the assumed bus voltage magnitude and its phase angle equal to the slack bus quantities |V1| = 1.0, δ1 = 0⁰.
- Compute Pi and Qi for each load bus from the following equation (5) and (6) shown above.
- Now, compute the scheduled errors ΔPi and ΔQi for each load bus from the following relations given below.
- For PV buses, the exact value of Qi is not specified, but its limits are known. If the calculated value of Qi is within the limits only ΔPi is calculated. If the calculated value of Qi is beyond the limits, then an appropriate limit is imposed and ΔQi is also calculated by subtracting the calculated value of Qi from the appropriate limit. The bus under consideration is now treated as a load bus.
- Compute the elements of the Jacobian matrix.
- Obtain the value of Δδ and Δ|Vi| from the equation shown below.
- Using the values of Δδi and Δ|Vi| calculated in the above step, modify the voltage magnitude and phase angle at all load buses by the equations shown below.
- Start the next iteration cycle following the step 2 with the modified values of |Vi|and δi.
- Continue until scheduled errors for all the load buses are within a specified tolerance that is
Where, ε denotes the tolerance level for load buses.
- Calculate the line and power flow at the slack bus same as in the Gauss Seidel method.
Advantages of Newton Raphson Method
The various advantages of Newton Raphson Method are as follows:-
- It possesses quadratic convergence characteristics. Therefore, the convergence is very fast.
- The number of iterations is independent of the size of the system. Solutions to a high accuracy is obtained nearly always in two to three iterations for both small and large systems.
- The Newton Raphson Method convergence is not sensitive to the choice of slack bus.
- Overall, there is a saving in computation time since fewer number of iterations are required.
Limitations of Newton Raphson Method
The various limitations are given below.
- This solution technique is difficult.
- It takes longer time as the elements of the Jacobian are to be computed for each iteration.
- The computer memory requirement is large.
Flowchart For Newton Raphson Method
The flowchart is drawn below for Newton Raphson Method using polar coordinates for load flow solutions.

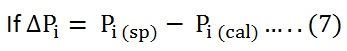
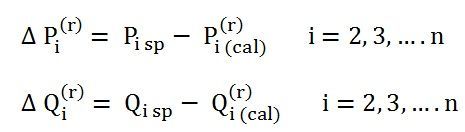
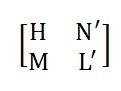
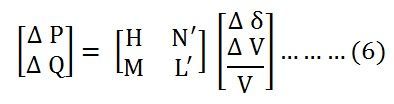
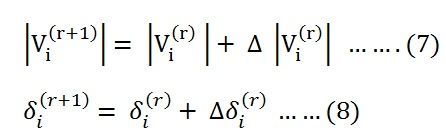
Good explanation 👍👍