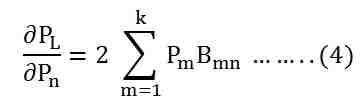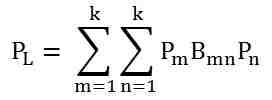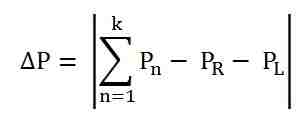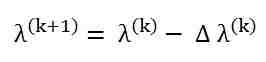The Iterative Method is a mathematical way of solving a problem which generates a sequence of approximations. This method is applicable for both linear and nonlinear problems with large number of variables. The word Iterative or Iteration refers to the technique that solve any linear system problems with successive approximation at each step. There are two methods under iterative methods one is stationary iterative method and another is a non stationary Iterative method.
Let us understand the iterative method with the help of an example.
The coordination equation for nth plant is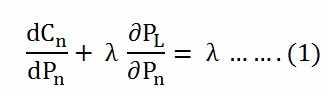
Let us assume that the plant has the quadratic cost functions of the form given below.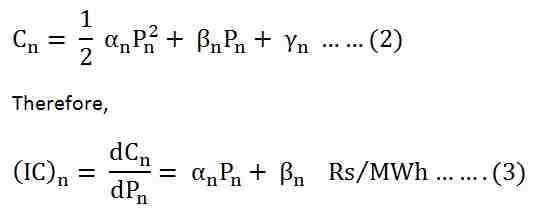
Where,
- αn is the slope of the incremental production cost curve.
- βn is the intercept of the incremental production cost curve on the (IC)n axis.
Thus, the equation (1) can be written as shown below.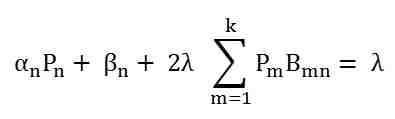
Collecting all the coefficient of Pn we get the following equation shown below.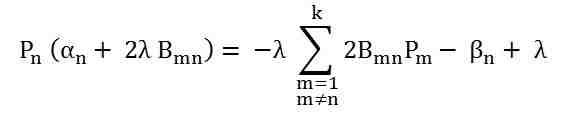
Solving for the value of Pn we will get.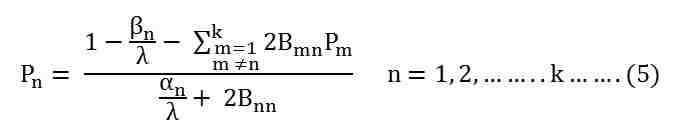
The above equation cannot be solved directly. It is solved by the Iterative method. The following procedure is given below to solve the equation by Iterative method.
- Assume the suitable value of λ = λ0. The incremental cost of the various units should be smaller greater than the intercept of the incremental cost of the various units. Calculate P1, P2 ….. Pn based on the equal incremental costs.
- Calculate the generation at all the buses with the help of equation (5). The values of powers to be substituted on the right hand side of the equation during zeroth iteration corresponds to the values calculated in the step 1.
- Check whether the difference between the power at all the generator buses and the two consecutive iterations should be less than a specified value. If not, then the step 2 is repeated again.
- Calculate the losses using the relation shown below.
- Now, calculate
- If ΔP is less than a specified value ε, stop the calculation and calculate the cost of generation with the values of powers. If ΔP < ε is not satisfied, then follow the step given below.
- Update λ as shown below
Where, Δλ is the step size. The step size Δλ may be selected on the basis of per unit power mismatch that is given as shown below.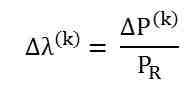
The initial guess and the step size are the two main considerations in any iterative solutions as the convergence and the number of Iteration depend on these two factors. Since the transmission losses are 10 to 15 percent of the total generation, the losses can be neglected for the initial guess in Iteration.