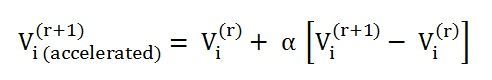Gauss-Seidel Method is used to solve the linear system Equations. This method is named after the German Scientist Carl Friedrich Gauss and Philipp Ludwig Siedel. It is a method of iteration for solving n linear equation with the unknown variables. This method is very simple and uses in digital computers for computing.
The Gauss-Seidel method is the modification of the gauss-iteration method.This modification reduces the number of iteration. In this methods the value of unknown immediately reduces the number of iterations, the calculated value replace the earlier value only at the end of the iteration. .Because of it, the gauss-seidel methods converges much faster than the Gauss methods. In gauss seidel methods the number of iteration method requires obtaining the solution is much less as compared to Gauss method.
Let us understand the Gauss-Seidel Method with the help of an example. Consider the total current entering the kth bus of an ‘n’ bus system is given by the equation shown below.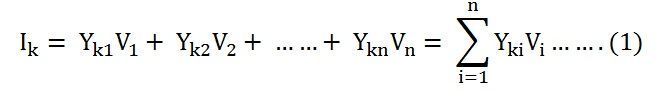
The complex power injected into the kth bus is given as![]()
The complex conjugate of the above equation becomes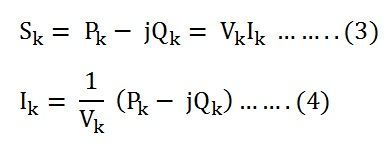
Elimination of Ik from the equation (1) and (4) gives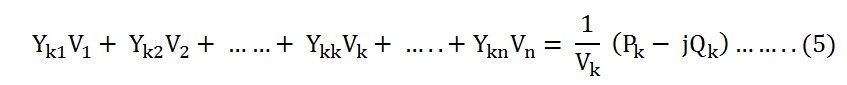
Therefore, the voltage at any bus ‘k’ where Pk and Qk are specified is given by the equation shown below.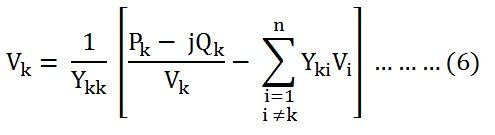
Equation (6) shown above is the major part of the iterative algorithm.
At the bus 2, the equation becomes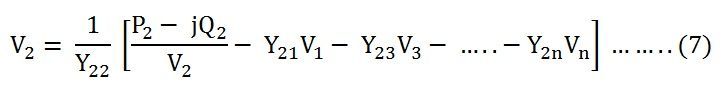
At the bus 3, the equation becomes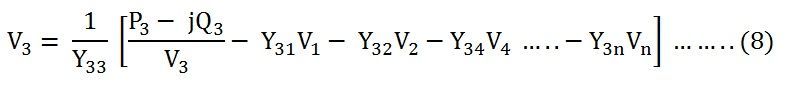
Now for the kth bus, the voltage at the (r + 1)th iteration is given by the equation shown below.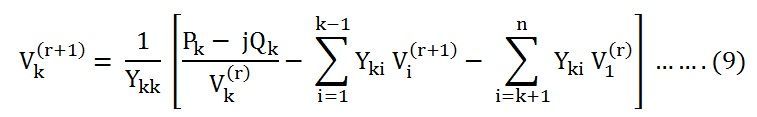
In the above equation, the quantities Pk, Qk, Ykk and Yki are known, and they do not vary during the iteration cycle.
Now the value of Ck and Dk are shown below, which is computed in the beginning, and it is used in every iteration step.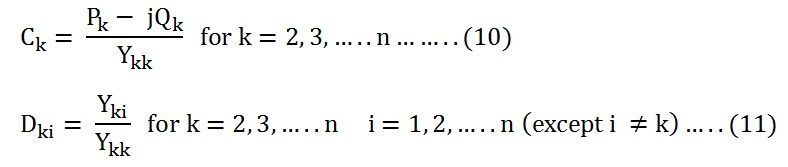
For the kth bus, the voltage at the (r + 1) th iteration can be written as shown below.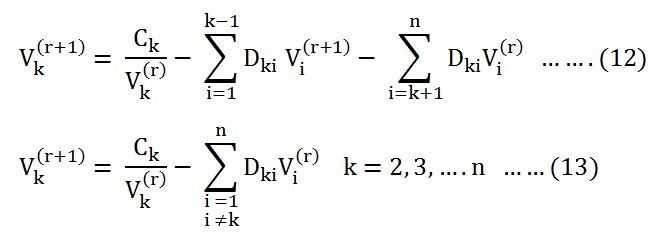
Acceleration Factors in Gauss-Seidel Method
In the Gauss-Seidel method, a large number of the iteration is required to arrive at the specified convergence. The rate of convergence can be increased by the use of the acceleration factor to the solution obtained after each iteration. The Acceleration factor is a multiplier that enhances correction between the values of voltage in two successive iterations.
Let us consider the acceleration Factor for the ith bus.
- Vi(r) is the value of the voltage at the rth iteration.
- Vi(r + 1) is the value of the voltage at the (r + 1)th iteration.
- Vi( accelerated)(r + 1) is the accelerated new value of the voltage at the (r+ 1) th iteration.
- r is the iteration count
- α is the accelerating factor
Thus, after calculating Vi(r + 1) at ( r + 1)th iteration, we calculate the value of new estimated bus voltage Vi( accelerated)(r + 1) and this new value replaces the previously calculated value. For real and imaginary components of the voltage different accelerating factors are used.
If Vi is resolved into real and imaginary components as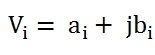
If α and β are the acceleration factor associated with ai and bi then the equation becomes as shown below.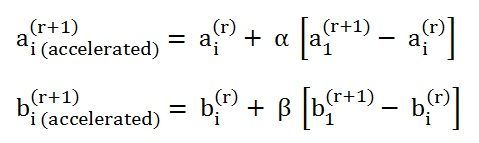
The choice of a specific value of the acceleration factor depends upon the system parameters. The optimum value of α usually lies in the range of 1.2 to 1.6 for most of the systems.