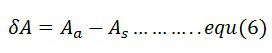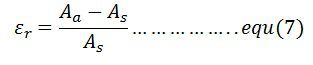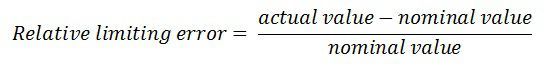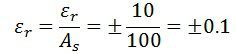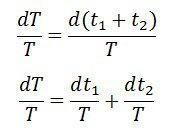Definition: The limited deviation of the measured value from the true value is known as the limiting error or guarantee error. Such type of error is fixed on the instrument. The magnitude of the limiting error depends on the design, material and the workmanship used for the construction of the instrument.
For obtaining a high degree of accuracy the high-quality material and workmanship are used. The instrument always has some amount of limiting error. The value of the limiting error could be least but never be zero.
The component like resistor, inductor and capacitor uses in the instrument has some rated fixed value. The deviation from their rated value causes the error in the system. The deviation mainly occurs because of the variation in the environmental condition. The manufacturer already knew about the limiting error of the instrument.
The actual value of the instrument along with the limiting error is expressed as![]()
Where,
Aa – actual value
As – specified or rated value
δA – limiting error or tolerance
Relative Limiting Error or Fractional Error
The relative limiting error is defined as the ratio of the limiting error to the nominal value of the measuring quantity. It is expressed as 
From equation (2) and (3) the limiting values are,
The equation below gives the percentage limiting error,
In limiting error, the specified quantity is taken as the true quantity, and the maximum deviation quantity is known as the incorrect or erroneous quantity.
For example – The nominal value of the resistor is 100 ohms. And the limiting error of the resistance is ±10 ohms. The magnitude of the actual value of the resistance lies between the Aa ≥ 90 ohms and Aa ≤110 ohms.
Or we can say that the magnitude of the limiting error lies between the 90 to 110 ohms.
Now consider that the nominal value As = 100Ω and δA = ±10Ω
and limiting value of resistance is,![]()
Combination of quantities with Limiting Error
When two or more quantities have limited error, it is more beneficial to compute their limiting error in combinations. The magnitude of the limiting error can easily be determined if the final result of the error is in the form of an algebraic equation.
Sum of two quantities – The T be the final result which is the sum of the measured quantities t1 and t2.![]()
The relative increment of the function is expressed as
Difference of two quantities – Let T be the resultant quantities and t1 and t2 are the measured quantities.![]()
The relative differences between two quantities 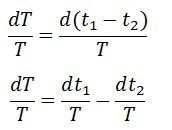 Sum or difference of two or more quantities – Consider the t1, t2, t3, and t4 are the four quantities,
Sum or difference of two or more quantities – Consider the t1, t2, t3, and t4 are the four quantities,![]()
the relative limiting error is 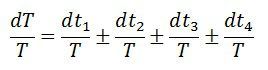 Similarly, the product or quotient of two or more quantities can be done.
Similarly, the product or quotient of two or more quantities can be done.