In Delta (Δ) or Mesh connection, the finished terminal of one winding is connected to start terminal of the other phase and so on which gives a closed circuit. The three-line conductors are run from the three junctions of the mesh called Line Conductors.
The connection in delta form is shown in the figure below:
Contents:
- Relation Between Phase Voltage and Line Voltage in Delta Connection
- Relation Between Phase Current and Line Current in Delta Connection
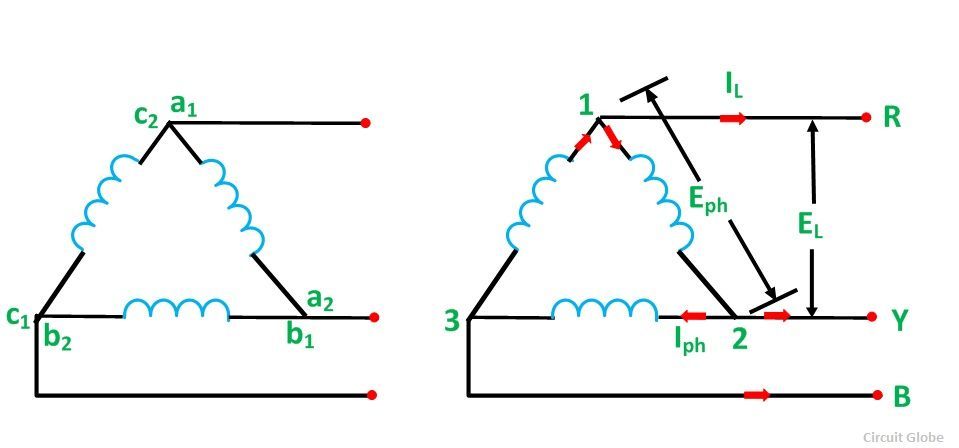
To obtain the delta connections, a2 is connected with b1, b2 is connected with c1 and c2 is connected with a1 as shown in the above figure. The three conductors R, Y and B are running from the three junctions known as Line Conductors.
The current flowing through each phase is called Phase Current (Iph), and the current flowing through each line conductor is called Line Current (IL).
The voltage across each phase is called Phase Voltage (Eph), and the voltage across two line conductors is called Line Voltage (EL).
Relation Between Phase Voltage and Line Voltage in Delta Connection
To understand the relationship between the phase voltage and line voltage in the delta connection, consider figure A shown below:
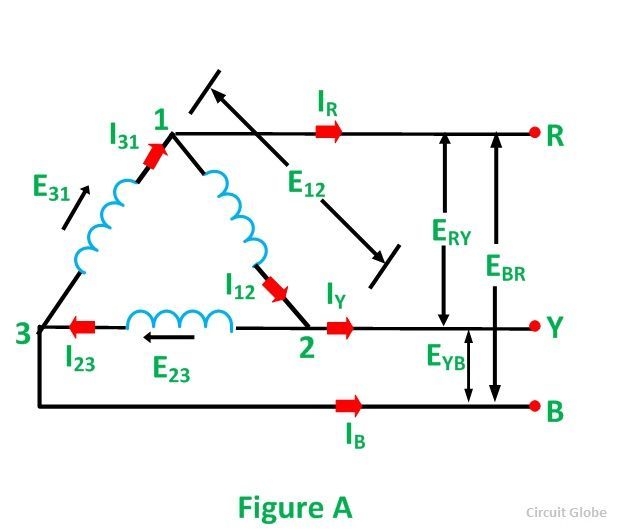 It is clear from the figure that the voltage across terminals 1 and 2 is the same as across the terminals R and Y. Therefore,
It is clear from the figure that the voltage across terminals 1 and 2 is the same as across the terminals R and Y. Therefore,
Similarly,
: the phase voltages are
The line voltages are:
Hence, in delta connection line voltage is equal to phase voltage.
Relation Between Phase Current and Line Current in Delta Connection
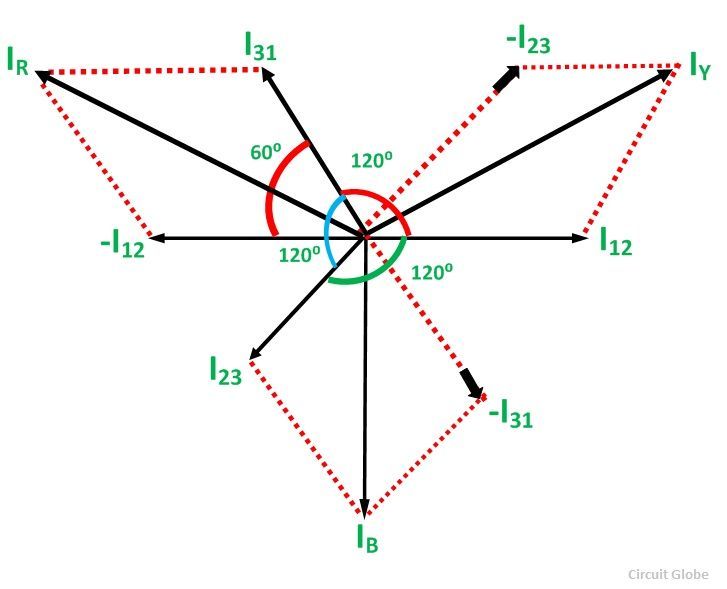
As in the balanced system the three-phase current I12, I23 and I31 are equal in magnitude but are displaced from one another by 120° electrical.
The phasor diagram is shown below:
If we look at figure A, it is seen that the current is divided at every junction 1, 2 and 3.
Applying Kirchhoff’s Law at junction 1,
The Incoming currents are equal to outgoing currents.
And their vector difference will be given as:
The vector I12 is reversed and is added in the vector I31 to get the vector sum of I31 and –I12 as shown above in the phasor diagram. Therefore,
As we know, IR = IL, therefore,
Similarly,
Hence, in delta connection line current is root three times of phase current.
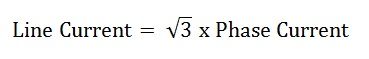
This is all about Delta Connection In a 3 Phase System.

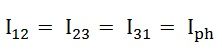
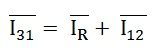
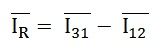
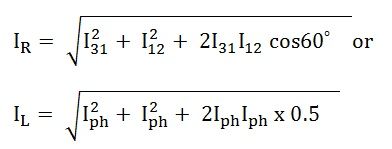
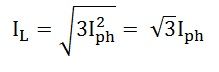
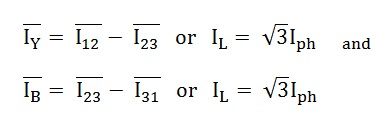
Please include phase angle for phase and line currents…..
Line current lagging 30° by phase current.
It’s very useful to us
Thanks for the information, very helpful to finish my pre-lab
Clear and perfect derivation,thank you!!