Definition: Cable capacitance is defined as the measurement of the electrical charges stored within it. The capacitor in the cable is constructed by two conductive material which is separated by an insulator or dielectric. The capacitance of the cable determines the charging current, charging KVA, and the dielectric loss.
The capacitance of a cable transmission line is very larger than that of an overhead line of the same length due to the following reasons.
- The distance between the conductor is very small.
- The distance between the core and earth sheath of the overhead line is very small.
- The permittivity of the cable insulation is usually 3 to 5 times greater than that of the insulation around the conductors of overhead line.
The capacitance of the overhead line is accurately calculated if their configuration is known. But for a cable such a calculation is approximate. The approximate method of cable calculation is based on the assumption that the cable dielectric is perfectly homogenous. But in actual practice, the insulation of cable are not homogeneous or uniform. The capacitance of a single core cable is found from the equation.
Capacitance of a three core belted cable
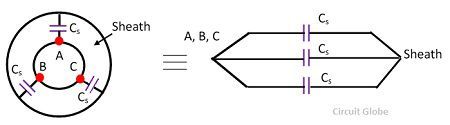
The conductor in a cable is separated from each other by the dielectric and there is a dielectric between the conductor and the sheath. When the potential difference is applied between the conductor of the cable, then due to potential difference there is a combination of six capacitances as shown in the figure below.
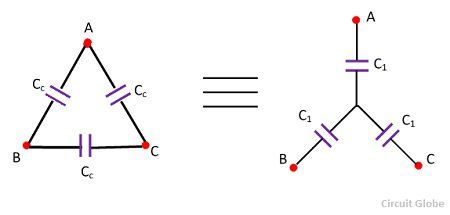
The capacitance between the conductors is represented by Cc while those between conductor and sheath by Cs.Thus, a three phase, belted cable may be represented by a system of capacitance connected in star and delta are shown below.
The delta-connected capacitances Cc may be replaced by star connected capacitance C1.The capacitance between pairs of terminals will be same in the two systems.
Capacitance between A and B in the delta system = Cc + 0.5Cs = 1.5Cc.
And the capacitance between A and B in the star system = 0.5 C1.
Of the two systems to be equivalent.
1.5 Cc = 0.5C1, C1 = 3Cc
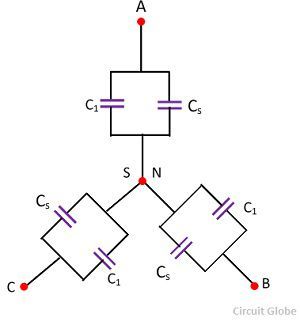
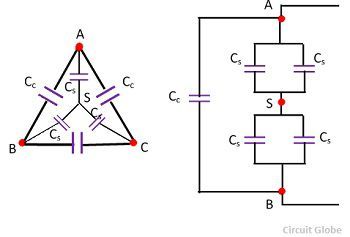
If the neutral point N of the system be earthed and the sheath is also at zero potential, N and S will become equipotential to that shown in the figure below.
Since C1 and Cs are in parallel they are combined into a single capacitance (C1 + C2).
The capacitance of each conductor to neutral or equivalent capacitance is given by
If VL = line voltage, Vp = phase voltage, the charging current per phase.
If to be noted that C0 is the capacitance between any conductor and screen for a 3-core screened cable.
Measurement of Cc and Cs
Cable capacitance is determined by actual capacitance. The variation in the shape of the conductor and the use of the filler makes it difficult to estimate the capacitance of the cable from its diameter. The following test is generally performed.
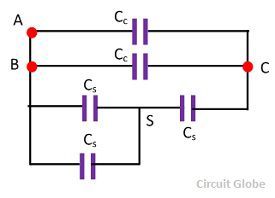
1.One conductor, say, C is connected to the sheath or insulated, and the capacitance is measured between the remaining two conductors A and B shown in the figure below.
The total capacitance CL measured between the cores A and B is
The single measurement is sufficient for calculating the charging current per conductor.
2. The three conductors are connected or bunched together, and the capacitance is measured between this bunch and the sheath. Let Cb denote it. Here Cc becomes zero and Cb = Cs.
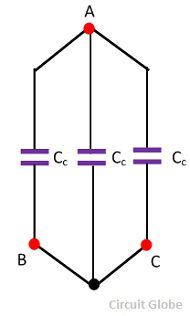
 3. Two conductors, say A and B, are joined and the capacitance is measured between them and the remaining conductor. The arrangement is shown in the figure below.
3. Two conductors, say A and B, are joined and the capacitance is measured between them and the remaining conductor. The arrangement is shown in the figure below.
4. Two conductors, B and C are connected to the sheath and the capacitance is measured between these and the third conductor A. The capacitance arrangement of the system, then reduces.
The capacitance measured is this case = Cs + Cc + Cc = 2Cc + Cs
From the above test, the value of Cc and Cs can also be determined separately.

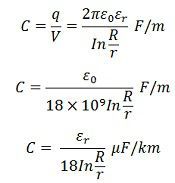


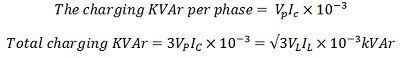
Very informative thanks