The Efficiency of the transformer is defined as the ratio of useful output power to the input power. The input and output power are measured in the same unit. Its unit is either in Watts (W) or KW. Transformer efficiency is denoted by Ƞ.
- V2 – Secondary terminal voltage
- I2 – Full load secondary current
- Cosϕ2 – power factor of the load
- Pi – Iron losses = hysteresis losses + eddy current losses
- Pc – Full load copper losses = I22Res
Consider, the x is the fraction of the full load. The efficiency of the transformer regarding x is expressed as
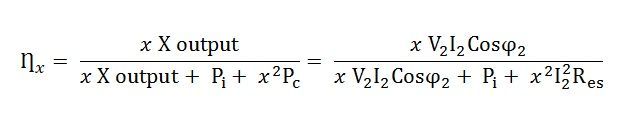 The copper losses vary according to the fraction of the load.
The copper losses vary according to the fraction of the load.
Maximum Efficiency Condition of a Transformer
The efficiency of the transformer along with the load and the power factor is expressed by the given relation:
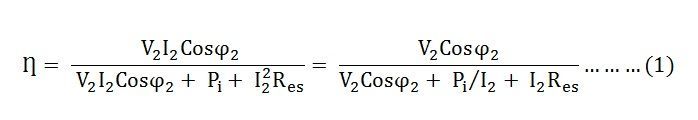 The value of the terminal voltage V2 is approximately constant. Thus, for a given power factor the Transformer efficiency depends upon the load current I2. In equation (1), the numerator is constant and the transformer efficiency will be maximum if the denominator with respect to the variable I2 is equated to zero.
The value of the terminal voltage V2 is approximately constant. Thus, for a given power factor the Transformer efficiency depends upon the load current I2. In equation (1), the numerator is constant and the transformer efficiency will be maximum if the denominator with respect to the variable I2 is equated to zero.
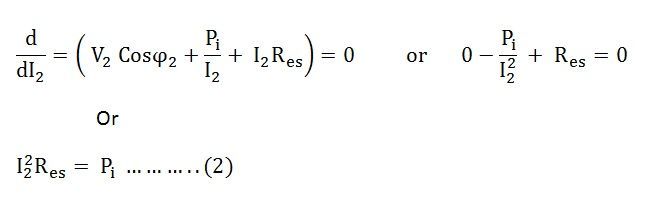 i.e Copper losses = Iron losses
i.e Copper losses = Iron losses
Thus, the transformer will give the maximum efficiency when their copper loss is equal to the iron loss.
From equation (2) the value of output current I2 at which the transformer efficiency will be maximum is given as
If x is the fraction of full load KVA at which the efficiency of the transformer is maximum then,
Copper losses = x2Pc (where Pc is the full load copper losses)
Iron losses = Pi
For maximum efficiency
Thus, output KVA corresponding to maximum efficiency

Putting the value of x from the above equation (3) in equation (4) we will get,
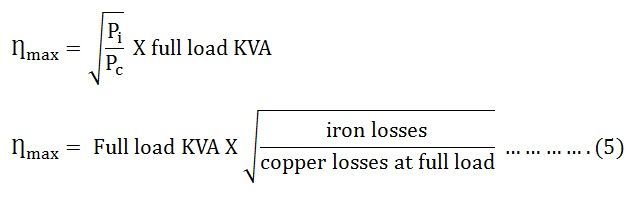 The above equation (5) is the maximum efficiency condition of the transformer.
The above equation (5) is the maximum efficiency condition of the transformer.


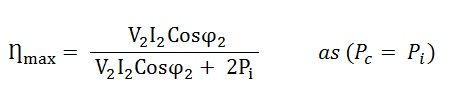
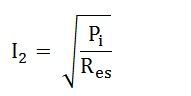
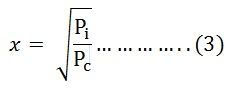
thanks for great works i found it useful .keep it up
Good work, I appreciate
It’s very nice. I like it
very good
Thanks for providing this.. Easy to understand.
It’s very interesting and understandable
Well done… Clearly Doubt cleared my confusion here…
Thanku for this. Easy to understand
brother this is mathematical expression but i want theoretical conditions
Very useful. Thank you so much for this.
Very interested
Very helpful, thanku so much
Very nice definition
Thanks for providing,I felt very easy to understand .