Efficiency is simply defined as the ratio of output power to the input power. Let R be the total resistance of the armature circuit (including the brush contact resistance, at series winding resistance, inter-pole winding resistance and compensating winding resistance).
The efficiency of the DC generator is explained below in the line diagram:
- I is the output current
- Ish is the current through the shunt field
- Ia is the armature current = I + Ish
- V is the terminal voltage.
Total copper loss in the armature circuit = Ia2Rat
Power loss in the shunt circuit = VIsh (this includes the loss in the shunt regulating resistance).
Mechanical losses = friction loss of bearings + friction loss at a commutator + windage loss.
Core losses = hysteresis loss + eddy current loss
Stray loss = mechanical loss + core loss
The sum of the shunt field copper loss and stray losses may be considered as a combined fixed (constant) loss that does not vary with the load current I.
Therefore, the constant losses (in shunt and compound generators) = stray loss + shunt field copper losses.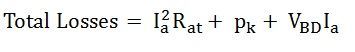
Generator efficiency is given by the equation shown below:
If Ish is small compared with Ir, then Ia = I
The efficiency ȠG will be a maximum when the denominator Dr is a minimum.
Since d2Dr/dI2 is positive, the expression is given by the equation (1) is a condition for the maximum value of Dr and the condition for the maximum value of efficiency.
Equation (1) shows that the efficiency of a DC generator is maximum when those losses proportional to the square of the load current are equal to the constant losses of the DC generator.
This relation applies equally well to all rotating machines, regardless of the type of machine.
This relationship is sometimes incorrectly stated as maximum efficiency occurs when the variable losses are equal to the constant losses.
Load Corresponding to Maximum Efficiency
Let,
- Ifl be the full load current,
- IM is the current at maximum efficiency
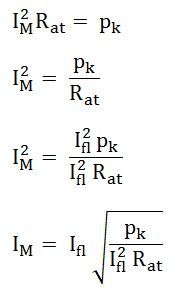 For maximum efficiency, therefore, the current at maximum efficiency is given by the equation shown below:
For maximum efficiency, therefore, the current at maximum efficiency is given by the equation shown below: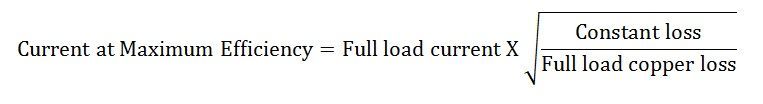
This is all about Efficiency of DC Generator.

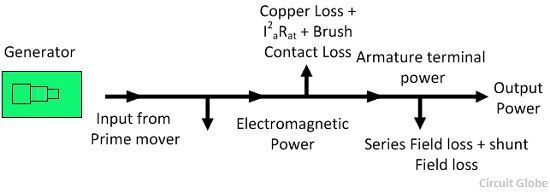
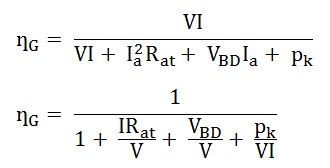
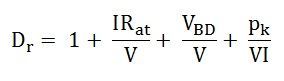
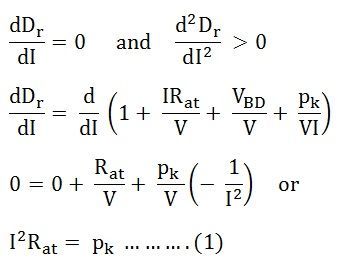
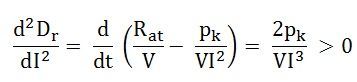
Pk instance for what?
Can you define all abrevaiation you used in the formulas stated.. Thanks