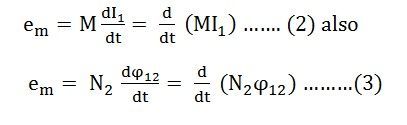Definition: Mutual Inductance between the two coils is defined as the property of the coil due to which it opposes the change of current in the other coil, or you can say in the neighbouring coil. When the current in the neighbouring coil changes, the flux sets up in the coil and because of this, changing flux emf is induced in the coil called Mutually Induced emf and the phenomenon is known as Mutual Inductance.
Let us understand the phenomenon of Mutual Inductance by considering an example as shown in the above figure.
Two coils namely coil A and coil B are placed nearer to each other. When the switch S is closed, and the current flows in the coil, it sets up the flux φ in the coil A and emf is induced in the coil and if the value of the current is changed by varying the value of the resistance (R), the flux linking with the coil B also changes because of this changing current.
Thus this phenomenon of the linking flux of the coil A with the other coil, B is called Mutual Inductance.
For determining the Mutual Inductance between the two coils, the following expression is used
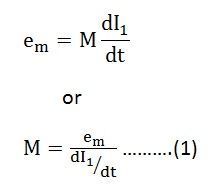
This expression is used when the magnitude of mutually induced emf in the coil and the rate of change of current in the neighbouring coil is known.
If em = 1 volt and dI1/dt = 1 ampere then putting this value in the equation (1) we get the value of mutual inductance as M=1 Henry
Hence, from the above statement, you can define Mutual Inductance as “the two coils are said to have a mutual inductance of one Henry if an emf of 1 volt is induced in one coil or say primary coil when the current flowing through the other neighbouring coil or secondary coil is changing at the rate of 1 ampere/second”.
Mutual inductance can also be expressed in another way as shown below
Equating equation (2) and (3) you will get
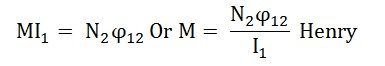
The above expression is used when the flux linkage (N2φ12) of one coil due to the current (I1) flowing through the other coil are known.
The value of Mutual Inductance (M) depends upon the following factors
- Number of turns in the secondary or neighboring coil
- Cross-sectional area
- Closeness of the two coils
Mutual Coupling In the Magnetic Circuit
When on a magnetic core, two or more than two coils are wound, the coils are said to be mutually coupled. The current, when passed in any of the coils wound around the magnetic core, produces flux which links all the coils together and also the one in which current is passed. Hence, there will be both self-induced emf and mutual induced emf in each of the coils.
The best example of the mutual inductance is the transformer, which works on the principle of Faraday’s Law of Electromagnetic Induction.
Faraday’s law of electromagnetic induction states that “ the magnitude of voltage is directly proportional to the rate of change of flux.” which is explained in the topic Faraday’s Law of Electromagnetic Induction.