Definition: – Synchronizing Power is defined as the varying of the synchronous power P on varying in the load angle δ. It is also called the Stiffness of Coupling, Stability or Rigidity factor. It is represented as Psyn. A synchronous machine, whether a generator or a motor, when synchronized to infinite busbars has an inherent tendency to remain in synchronism.
Consider asynchronous generator transferring a steady power Pa at a steady load angle δ0. Suppose that, due to a transient disturbance, the rotor of the generator accelerates, resulting from an increase in the load angle by dδ. The operating point of the machine shifts to a new constant power line and the load on the machine increases to Pa + δP. The steady power input of the machine does not change, and the additional load which is added decreases the speed of the machine and brings it back to synchronism.
Similarly, if due to a transient disturbance, the rotor of the machine retards resulting a decrease in the load angle. The operating point of the machine shifts to a new constant power line and the load on the machine decreases to (Pa – δP). Since the input remains unchanged, the reduction in load accelerates the rotor. The machine again comes in synchronism.
The effectiveness of this correcting action depends on the change in power transfer for a given change in load angle. The measure of effectiveness is given by Synchronising Power Coefficient.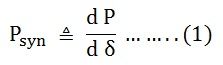
Power output per phase of the cylindrical rotor generator synchronizing torque coefficient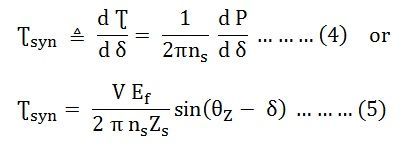
In many synchronous machines Xs >> R. Therefore, for a cylindrical rotor machine, neglecting saturation and stator resistance equation (3) and (5) become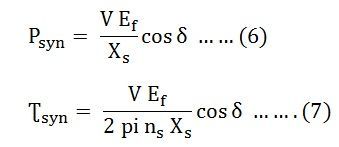
Unit of Synchronizing Power Coefficient Psyn
The synchronizing power coefficient is expressed in watts per electrical radian.
Since, π radians = 180⁰
If P is the total number of pair of poles of the machine.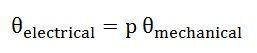
Synchronising Power Coefficient per mechanical radian is given by the equation shown below: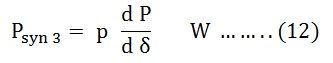
Synchronising Power Coefficient per mechanical degree is given as: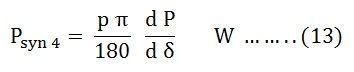
Synchronising Torque Coefficient
Synchronising Torque Coefficient gives rise to the synchronising torque coefficient at synchronous speed. That is, the Synchronizing Torque is the torque at which synchronous speed gives the synchronising power. If Ʈsyn is the synchronising torque coefficient then the equation is given as shown below: Where,
Where,
- m is the number of phases of the machine
- ωs = 2 π ns
- ns is the synchronous speed in revolution per second
Significance of Synchronous Power Coefficient
The Synchronous Power Coefficient Psyn is the measure of the stiffness between the rotor and the stator coupling. A large value of Psyn indicates that the coupling is stiff or rigid. Too rigid a coupling means and the machine will be subjected to shock, with the change of load or supply. These shocks may damage the rotor or the windings. We have,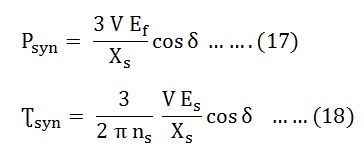
The above two equations (17) and (18) show that Psyn is inversely proportional to the synchronous reactance. A machine with large air gaps has relatively small reactance. The synchronous machine with the larger air gap is stiffer than a machine with a smaller air gap. Since Psyn is directly proportional to Ef, an overexcited machine is stiffer than an under excited machine.
The restoring action is great when δ = 0, that is at no load. When the value of δ = ± 90⁰, the restoring action is zero. At this condition, the machine is in unstable equilibrium and at a steady-state limit of stability. Therefore, it is impossible to run a machine at the steady-state limit of stability since its ability to resist small changes is zero unless the machine provided with a special fast-acting excitation system.


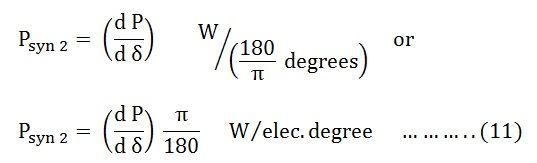

THANK YOU … IT WAS A NICE EXPLANATION ….
Thanks, nice explanation.