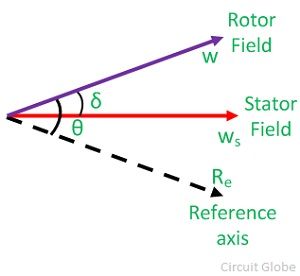
The transient stability of the system can be determined by the help of the swing equation. Let θ be the angular position of the rotor at any instant t. θ is continuously changing with time, and it is convenient to measure it with respect to the reference axis shown in the figure below. The angular position of the rotor is given by the equation
Where,
θ – angle between rotor field and a reference axis
ws – synchronous speed
δ – angular displacement
Differentiation of equation (1) gives
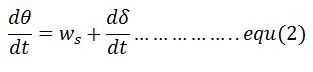Differentiation of equation (2) gives
Angular acceleration of rotor
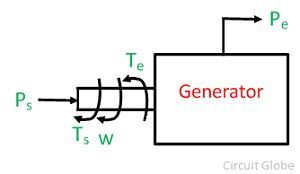
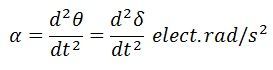Power flow in the synchronous generator is shown in the diagram below. If the damping is neglected the accelerating torques, Ta in a synchronous generator is equal to the difference of mechanical input shaft and the electromagnetic output torque, i.e.,
Where,
Ta – accelerating torque
Ts – shaft torque
Te – electromagnetic torque
Angular momentum of the rotor is expressed by the equation
Where,
w- the synchronous speed of the rotor
J – moment of inertia of the rotor
M – angular momentum of the rotor
Multiplying both the sides of equation (5) by w we get
Where,
Ps – mechanical power input
Pe – electrical power output
Pa – accelerating power
But,
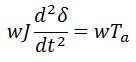
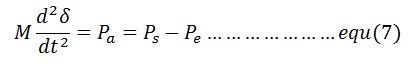Equation (7) gives the relation between the accelerating power and angular acceleration. It is called the swing equation. Swing equation describes the rotor dynamics of the synchronous machines and it helps in stabilizing the system.
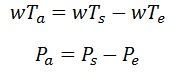
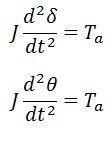
Thanks for your detailed explanation
thank you so much it is so easy to understand well may god bless u