Definition: Numerical Aperture is the measure of the ability of an optical fiber to collect or confine the incident light ray inside it. It is among the most basic property of optical fiber.
Numerical aperture is abbreviated as NA and shows the efficiency with which light is collected inside the fiber in order to get propagated.
We know light through an optical fiber is propagated through total internal reflection. Or we can say multiple TIR takes place inside the optical fiber for the light ray to get transmitted from an end to another through an optical fiber.
Basically when the light is emitted from an optical source, then the fiber must be highly efficient so as to collect the maximal emitted radiation inside it.
Thus we can say that the light gathering efficiency of an optical fiber is the key characteristic while transmitting a signal through an optical fiber.
NA is related to acceptance angle. As acceptance angle is that max angle through which light enters the fiber. Hence the acceptance angle and numerical aperture are related to each other.
Propagation through Optical fiber
As we have already discussed that light through an optical fiber is propagated by several continuous total internal reflections.
As we know that an optical fiber is composed of a core which is made up of a very pure form of glass silica and is surrounded by a glass cladding. So, the light is propagated inside the fiber by performing continuous reflections from the cladding.
But the condition of total internal reflection for the propagation of light ray comes into action only when most of the light is collected inside the fiber. So, let us now understand the numerical aperture for optical fiber in detail.
Derivation for Numerical Aperture of Optical Fiber
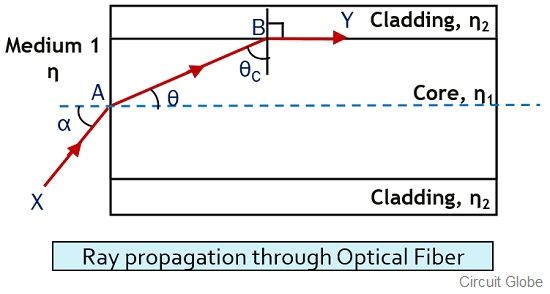
Consider a light ray XA, that incident inside the optical fiber. The refractive index of the core is ƞ1 and that of cladding is ƞ2.
The figure below shows an optical fiber inside which light ray is focused.
So, the ray XA is launched from denser medium to rarer medium by making an angle α with the fiber axis. This angle α is known as the acceptance angle of the fiber.
This incident ray propagates inside the fiber and gets reflected completely by the core-cladding interface.
But for this, the angle of the incident should be more as compared to the critical angle. Otherwise, if the incident angle is less the critical angle then rather being reflected, the ray gets refracted.
According to Snell’s law, the incident and refracted ray propagate in the same plane. Hence, on applying Snell’s law at medium 1 (usually air) and core interface. Then
From the above figure, we can write
On putting the value of θ from the above equation in equation 1, we get,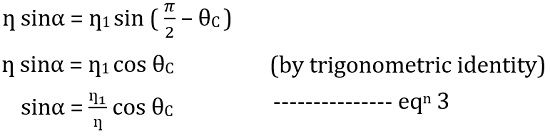
Applying Snell’s law at core-cladding interface, we get
Substituting the above value in equation 4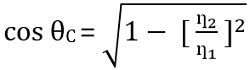
Substituting the above value in equation 3, we get
As we have already discussed that medium 1 is air, thus refractive index i.e., ƞ will be 1.
So more specifically we can say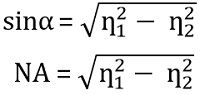
This is the expression for the numerical aperture of an optical fiber, having ƞ1 as the refractive index of core and ƞ2 as the refractive index of the cladding.
So we can conclude that as the numerical aperture shows the light collecting ability of the fiber thus its value must be high. As higher the value of NA, better will be the optical fiber.
However, the greater value of NA will be achieved only when the difference between the two refractive indices is high and for this either, ƞ1 is to be high or ƞ2 to be low.
But no such material exists that has lower refractive index than 1. So, an option stands that if we remove the cladding present over the core then greater NA can be achieved.
While, for optical signal propagation, the only motive is not to have high accepting range but also to propagate the accepted signal with minimal attenuation.
This is so because an optical fiber that has the greatest light gathering efficiency but does not allow light propagation through it properly, is not of any use.
Thus several parameters must be taken into consideration, for selecting the appropriate optical fiber for signal propagation.

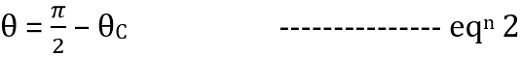
Nice explanation of the numerical aperture.
Thanks.
Well explained
Nice explanation maam
Thanks. I was able to turn in my assignment on time due to this 🙂
Thnx….i loved the explanation ♥
Superb content
Nice 👍