Definition: In digital electronics, the number system is used for representing the information. The number system has different bases and the most common of them are the decimal, binary, octal, and hexadecimal. The base or radix of the number system is the total number of the digit used in the number system. Suppose if the number system representing the digit from 0 – 9 then the base of the system is the 10.
Types of Number Systems
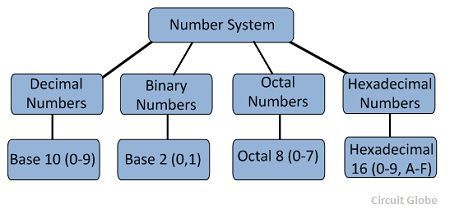
Some of the important types of number system are
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System
These number systems are explained below in details.
 1. Decimal Number Systems
1. Decimal Number Systems
The number system is having digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; this number system is known as a decimal number system because total ten digits are involved.The base of the decimal number system is 10.
2. Binary Number Systems
The modern computers do not process decimal number; they work with another number system known as a binary number system which uses only two digits 0 and1.The base of binary number system is 2 because it has only two digit 0 and 1.The digital electronic equipments are works on the binary number system and hence the decimal number system is converted into binary system.
The table is shown below the decimal, binary, octal, and hexadecimal numbers from 0 to 15 and their equivalent binary number.
| Decimal | Binary | Octal | Hexadecimal |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
3. Octal Numbers
The base of a number system is equal to the number of digits used, i.e., for decimal number system the base is ten while for the binary system the base is two. The octal system has the base of eight as it uses eight digits 0, 1, 2, 3, 4, 5, 6, 7.
All these digits from 0 to 7 have the same physical meaning as by decimal symbols, the next digit in the octal number is represented by 10, 11, 12, which are equivalent to decimal digits 8, 9, 10 respectively. In this way, the octal number 20 will represent the decimal digit and subsequently, 21, 22, 23.. Octal numbers will represent the decimal number digit 17, 18, 19… etc. and so on.
4. Hexadecimal Numbers
These numbers are used extensively in microprocessor work.The hexadecimal number system has a base of 16, and hence it consists of the following sixteen number of digits.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
The size of the hexadecimal is much shorter than the binary number which makes them easy to write and remember. Let 0000 to 000F representing hexadecimal numbers from zero to fifteen, then 0010, 0011, 0012, …etc. Will represent sixteen, seventeen, eighteen… etc. till 001F which represent thirty open and so on.

Nice one
Really good
thank you.
simple and nice
Thanks 😊
THANK YOU
Thank you 🙂
THANKS FOR THIS BEAUTIFULLY YET SIMPLE WRITTEN POST.
Thank you 😊
Thank you very much
Awesome 😊
Thank you so much