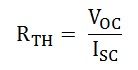Thevenin’s theorem gives the mathematical technique of replacing the given network by a single voltage source by a resistance in series. The different methods of finding Thevenin’s Resistance or internal impedance are as follows:
For Independent Sources – The most common method of finding the equivalent Thevenin’s Resistance (RTH) or the internal impedance of any linear, bilateral network containing independent current or voltage source is to deactivate the source by its internal resistance.
For the independent current source, it is deactivated by removing the source. Similarly, for the voltage source, it is deactivated by short-circuiting it. Assuming the internal resistance of the voltage source is zero, further we find the internal resistance of the network looking through the load terminals and keeping it open-circuited.
For Dependent Source – For calculating the internal impedance of the dependent source in addition to or in the absence of independent source, the methods are as follows:
First Method:
First of all, find open-circuit voltage Voc across the load terminals by the conventional method either by mesh or nodal analysis. Now, short circuit the load terminals and find the short circuit current (ISC) through the shorted terminals. The equivalent resistance of the source network is then obtained by the equation given below:
Second Method:
The one more method to find the internal impedance is firstly removed the load resistance and apply a DC driving voltage Vdc at the open-circuited load terminals. Keep the other independent sources deactivated when a direct current is applied to the load terminal. This means that the voltage source terminals are short-circuited, and the current source is open-circuited.
When the voltage is applied by the DC supply to the load terminal, a DC driving current idc starts flowing in the circuit of the load terminals. This is because of the application of the vdc. The internal impedance of the source network is obtained by the equation given below:
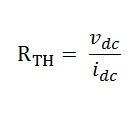
Hence, this is all about methods of finding RTH.