Calculation of sag and tension in transmission line depend on the span of the conductor. Span having equal level supports is called level span, whereas when the level of the supports is not at an equal level is known as unequal level span. The calculation of conductor at an equal level shown below.
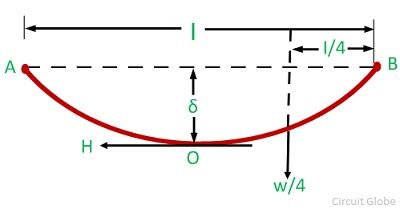
Consider a conductor AOB suspended freely between level supports A and B at the same level.The lowest point of the conductor is O. Let the shape of the conductor be a parabola.
l – span length
w- weight per unit length of the conductor
δ – conductor sag
H – tension in the conductor at the point of maximum deflection O
TB – tension in the conductor at the point of support B.
Consider OB is the equilibrium tension of the conductor and force acting on it are the horizontal tension H at O. The weight (w.OB) of the conductor OB acting vertically downwards through the center of gravity at a distance l/4 from B, and the tension TB at the support B.
![]() Since OB is approximately equal to the l/2
Since OB is approximately equal to the l/2
Take moments about B
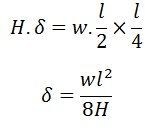 Above equation shows that the sag in a freely suspended conductor is directly proportional to the weight per unit length of the conductor, and the square of the span length and inversely proportional to the horizontal tension H.
Above equation shows that the sag in a freely suspended conductor is directly proportional to the weight per unit length of the conductor, and the square of the span length and inversely proportional to the horizontal tension H.
Calculation of Sag and Tension at an unequal level supports
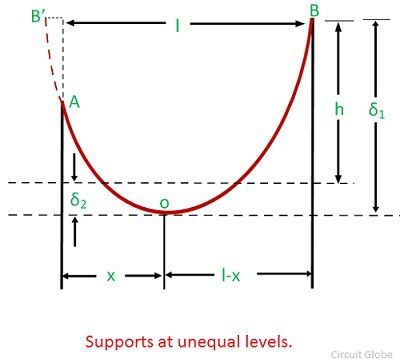
In hilly areas or sloping grounds, the supports are not usual at the same level. For the calculation of sag and tension at unequal supports level consider a conductor AOB. The portion of OA and OB may be treated as catenaries of half span x and l-x respectively shown in the figure below.
h – difference span length between A and B
l – horizontal span length between A and B
x – the horizontal distance of A from the lowest point O.
l – x – a horizontal distance of B from the lowest point O.
The sag at OA and OB is expressed by the equations
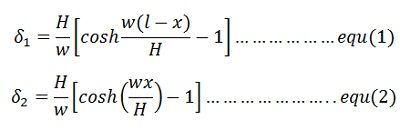 The tension A and B are given by
The tension A and B are given by
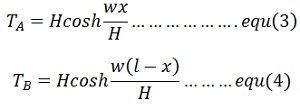 The maximum tension will occur at B since (l-x) is greater than x as seen in the figure above.
The maximum tension will occur at B since (l-x) is greater than x as seen in the figure above.
Vertical reaction at the higher support – w.(l-x)
Vertical reaction at lower support – w.x
For calculation, it is assumed that the AOB is the parabola.
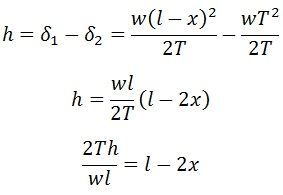
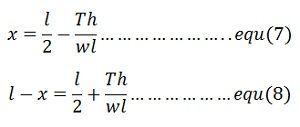 The value of x obtained above may be substituted in equation (5) to calculate sag at OA . Equation (8) shows that the lowest point lies outside the span AB. Hence, the conductor in the span under consideration exert an upward force, and the conductor tends to swing clear of the lower support.
The value of x obtained above may be substituted in equation (5) to calculate sag at OA . Equation (8) shows that the lowest point lies outside the span AB. Hence, the conductor in the span under consideration exert an upward force, and the conductor tends to swing clear of the lower support.

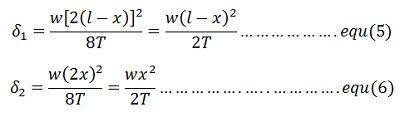
Great Article
Very good sir
Thanks for that
What is the exact formula to calculate sag……
I really helped me…thanx
Very useful, thank you mam!
Anybody ever use an iPhone to measure sag using the pulse return method?
perfectly explained
Good explanation
Very helpful. Thank you
Simply explained
What is the exact formula to calculate sag?
MANY THANKS