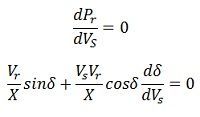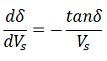Definition: Voltage stability in the power system is defined as the ability of a power system to maintain acceptable voltages at all bus in the system under normal condition and after being subjected to a disturbance. In the normal operating condition the voltage of a power system is stable, but when the fault or disturbance occurs in the system, the voltage becomes unstable this result in a progressive and uncontrollable decline in voltage. Voltage stability is sometimes also called load stability.
Due to the voltage instability, a power system may undergo voltage collapse, if the post-disturbance equilibrium voltage near loads is below acceptable limits. Voltage collapse is also defined as a process by which the voltage instability provides advantages of a very low voltage profile in the essential part of the system. Voltage collapse may be total or partial blackout. The terms voltage instability and voltage collapse are often used interchangeably.
Classification of Voltage Stability
Voltage stability may be classified into two categories. These are
- Large-disturbance Voltage Stability
- Small-disturbance Voltage Stability
Large-disturbance Voltage Stability – It is concerned with a system stability to control voltages following a large disturbance such as system faults, loss of load, or loss of generation. For determination of this form of stability requires the examination of the dynamic performance of the system over a period sufficient to capture of such devices as under load tap changing transformers, generator field, and current limiters. Large disturbance voltage studies can be studied by using non-linear time domain simulations which include proper modeling.
Small-Disturbances Voltage Stability – The operating state of a power system is said to have small disturbances voltage stability if the system has small disturbances, a voltage near loads does not change or remain close to the pre-disturbance values. The concept of small disturbance stability is related to steady state and be analyzed using a small-signal model of the system.
Voltage Stability Limit
The Voltage stability limit can be defined as the limiting stage in a power system beyond which no amount of reactive power injection will raise the system voltage to its nominal state. The system voltage can only be adjusted by reactive power injections till the system voltage stability is maintained.
The power transfer over a lossless line is given by:
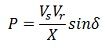 where P = power transferred per phase
where P = power transferred per phase
Vs = sending-end phase voltage
Vr = receiving-end phase voltage
X = transfer reactance per phase
δ = phase angle between Vs and Vr.
Since the Line is lossless
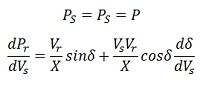 Assuming the power generation to be constant,
Assuming the power generation to be constant,
δ = 90º, so that as δ→∞
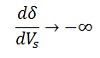 Above equation gives the location of the critical point on the δ versus Vs curve. It is assumed that the receiving end voltage is constant.
Above equation gives the location of the critical point on the δ versus Vs curve. It is assumed that the receiving end voltage is constant.
The Similar result can be obtained assuming the sending end voltage constant and analyzing the system taken Vr as a variable parameter. In this case, the resultant equation is
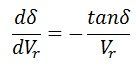 The reactive power expression at the receiving-end bus may be written as
The reactive power expression at the receiving-end bus may be written as
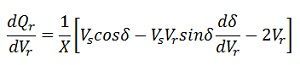 On substituting the value of ds/dVr from equation, we get
On substituting the value of ds/dVr from equation, we get
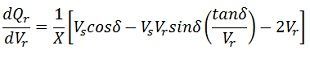
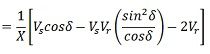
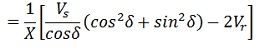 Or
Or 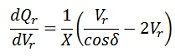 At the steady-state power angle stability, δ = 90º so that as δ→∞
At the steady-state power angle stability, δ = 90º so that as δ→∞
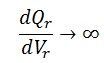 Above equation represents steady-state voltage stability limit. It shows that, at steady state stability limit, the reactive power becomes infinite. This means that dQ/dVr becomes zero. Hence the rotor angle stability limit under steady state conditions is coincident with steady state voltage stability limit. The voltage stability at steady state is also affected by the load.
Above equation represents steady-state voltage stability limit. It shows that, at steady state stability limit, the reactive power becomes infinite. This means that dQ/dVr becomes zero. Hence the rotor angle stability limit under steady state conditions is coincident with steady state voltage stability limit. The voltage stability at steady state is also affected by the load.