Metadyne is a special machine which consists of two pairs of brushes or has an additional set of brushes on the d axis. This arrangement enables the armature MMF to provide most of the excitation and achieve higher power gains. In this, the brushes of the quadrature axis (q axis) are short-circuited, and direct axis (d axis) brushes give the output.
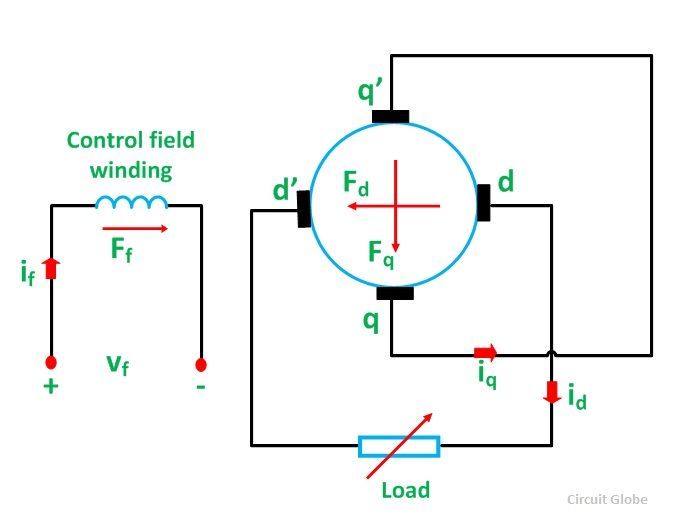
The schematic diagram of a Metadyne is shown below.
A stator of the machine has a control field winding. A current if flows through the control field winding. The generator is rotating at a constant speed; an EMF eaq is induced between the quadrature axis brushes qq’ because of the control field winding MMF.
This EMF is given by the equation shown below.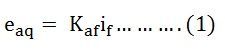
Where, Kaf is a constant and if is the field current.
The brushes qq’ are short-circuited, a quadrature axis armature current iq flows and establish an MMF Fq if the quadrature axis. Since the impedance of the short-circuited path is low, a small change in control field current produces a greater armature current in the q axis.
The magnetic field is stationary in space because of the commutator action. Rotation in the q axis flux produces an EMF in the armature. This EMF appears across the direct axis brushes dd’ and is given by the equation shown below.![]()
Where, Kdq is a constant and iq is the quadrature axis armature current.
If the load resistance RL is connected across the direct axis brushes, the direct axis armature current id will flow through the load. A direct axis flux Fd is produced by this current and according to Lenz’s law, it opposes its main cause, i.e., the control field MMF Ff.
The magnetic field of the current produced is 90 degrees ahead of the flux wave producing the voltage. Since, there are two stages of voltage generation, the MMF of the direct axis output current is shifted twice by 90 degrees. As a result, it opposes the control field MMF.
The voltage generated in the quadrature axis is given as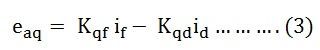
Where Kqd is a constant if the magnetic saturation is neglected and speed is assumed to be constant.
An increase in id decreases eaq and as a result, iq is reduced. Hence, ead and id are reduced. Thus, over a wide range of load variation the value of field excitation current if and the output current id remains constant. A Metadyne acts as a constant current generator.

It’s well equipped and has all that one requires