Binary to Decimal Conversion Methods

The decimal number system is represented by the digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. It consists ten digits and hence the base of the system is 10. Their base is increased by the factor of 10. On the other hand, the binary number system consists only two digits 1 and 0.The base of the binary number system is 2, and it is increased by the factor of two. The first digit has 2⁰ weights, the second has 2¹ weights, the weight of the third digit is 2² and so on. Consider a decimal number 3285 it can be written as

3285 = 3000 + 200 + 80 + 5
3285 = 3(10³) + 2(10²) + 8(10¹) + 5(10⁰)

Thus the decimal number system is an example of positional notation where each digit position has a weight in terms of powers of ten. Similarly, in the binary number system each digit position has a weight regarding powers of two. Some of the examples of a binary digit are shown in the example.

In binary to decimal conversion when there is one in a digit position of a binary number, then the weight of the position is added. But when there is the zero in a binary position the weight of the position is disregarded.

Considered the conversion of the binary number 10101 into its equivalent decimal numbers

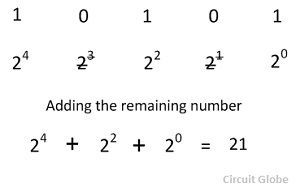On disregarding the weight 2³ and 2¹ and summing up the remaining weights, we get the equivalent decimal number 21.

Binary to Decimal Conversion for Fractional Number

For a fractional number, the weights of the digit position to the right of binary point are given by 2^-1, 2^-2, 2^-3, 2^-4… etc. Consider the conversion of a fractional binary number.0101 into its equivalent decimal numbers.

After disregarding the weight 2^-1 and 2^-3 and summing up the remaining weights, i.e., we get the decimal number 0.3125.

Binary to Decimal Conversion For Mixed Number

The number with an integer and fractional part are called mixed number.The weight for a mixed number can be written as

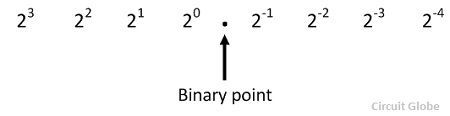Consider the conversion of a binary number 1101.101 into its equivalents decimal number

After disregarding the weight 2¹ and 2^-1 and on summing up the remaining weights the required decimal number is 13.625.