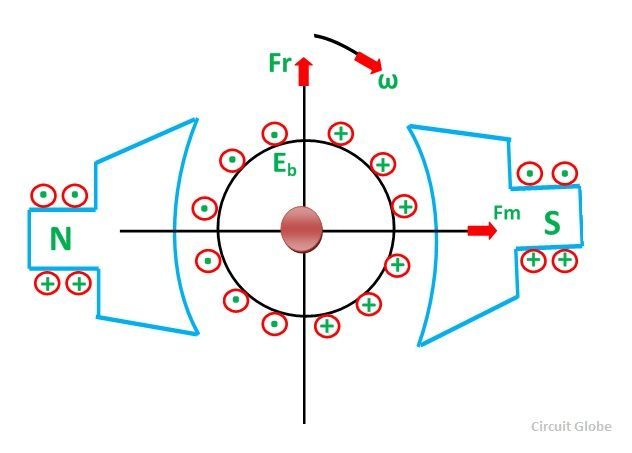
When the current-carrying conductor placed in a magnetic field, the torque induces on the conductor, the torque rotates the conductor which cuts the flux of the magnetic field. According to the Electromagnetic Induction Phenomenon “when the conductor cuts the magnetic field, EMF induces in the conductor”.
The Fleming right-hand rule determines the direction of the induced EMF.
According to Fleming Right Hand Rule, if we hold our thumb, middle finger and index finger of the right hand by an angle of 90°, then the index finger represents the direction of the magnetic field. The thumb shows the direction of motion of the conductor and the middle finger represents the emf induces on the conductor.
On applying the right-hand rule in the figure shown below, it is seen that the direction of the induced emf is opposite to the applied voltage. Thereby the emf is known as the counter emf or back emf.
The back emf is developed in series with the applied voltage, but opposite in direction, i.e., the back emf opposes the current which causes it.
The magnitude of the back emf is given by the same expression shown below:
Where Eb is the induced emf of the motor known as Back EMF, A is the number of parallel paths through the armature between the brushes of opposite polarity. P is the number of poles, N is the speed, Z is the total number of conductors in the armature and ϕ is the useful flux per pole.
A simple conventional circuit diagram of the machine working as a motor is shown in the diagram below:
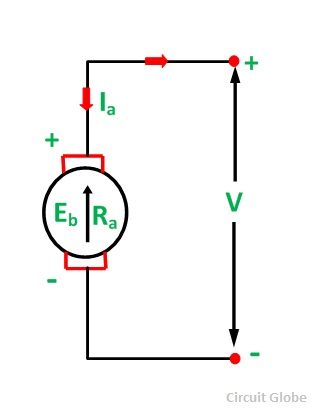 In this case, the magnitude of the back emf is always less than the applied voltage. The difference between the two is nearly equal when the motor runs under normal conditions.
In this case, the magnitude of the back emf is always less than the applied voltage. The difference between the two is nearly equal when the motor runs under normal conditions.
The current induces on the motor because of the main supply. The relation between the main supply, back emf and armature current is given as Eb = V – IaRa.
Advantages of Back Emf in DC Motor
1. The back emf opposes the supply voltage. The supply voltage induces the current in the coil which rotates the armature. The electrical work required by the motor for causing the current against the back emf is converted into mechanical energy. And that energy is induced in the armature of the motor. Thus, we can say that energy conversion in the DC motor is possible only because of the back emf.
The mechanical energy induced in the motor is the product of the back emf and the armature current, i.e., EbIa.
2. The back emf makes the DC motor self-regulating machine, i.e., the back emf develops the armature current according to the need of the motor. The armature current of the motor is calculated as:
Let’s understand how the back emf makes motor self-regulating.
- Consider the motor is running at no-load condition. At no load, the DC motor requires small torque for controlling the friction and windage loss. The motor withdraws less current. As the back emf depends on the current their value also decreases. The magnitude of the back EMF is nearly equal to the supply voltage.
- If the sudden load is applied to the motor, the motor becomes slow down. As the speed of the motor decreases, the magnitude of their back emf also falls down. The small back emf withdraw heavy current from the supply. The large armature current induces the large torque in the armature, which is the need of the motor. Thus, the motor moves continuously at a new speed.
- If the load on the motor is suddenly reduced, the driving torque on the motor is more than the load torque. The driving torque increases the speed of the motor which also increases their back emf. The high value of back emf decreases the armature current. The small magnitude of armature current develops less driving torque, which is equal to the load torque. And the motor will rotate uniformly at the new speed.
relation between Mechanical power (Pm), supply voltage (Vt) and Back EMF (Eb)
The back emf in the dc motor is expressed as:
Where Eb – Back Emf
Ia – Armature Current
Vt – Terminal Voltage
Ra – Resistance of Armature
The maximum power developed on the motor is expressed by
On differentiating the above equation we get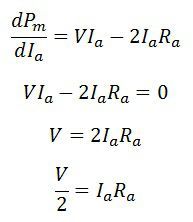
From the back emf equation, we get
On substituting the IaRa in the above equation, we get
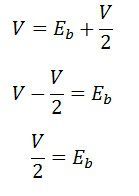 The above equation shows that the maximum power is developed in the motor when the back emf is equal to half of the supply voltage.
The above equation shows that the maximum power is developed in the motor when the back emf is equal to half of the supply voltage.

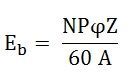
How is the length of armature conductor related to the back emf ? Is the back emf equation presented as E = nBLV. E = back emf ; n = number of conductors ; B = Flux Density ; L = length of conductor ; V = rotational velocity
back emf is not related to the length of the armature conductor.
As we increase the length of conductor .
So obviously turns of winding on armature increase.
That’s why back emf production is also increase.
Very clear explanation mam… Tq
Great and simplified explanation