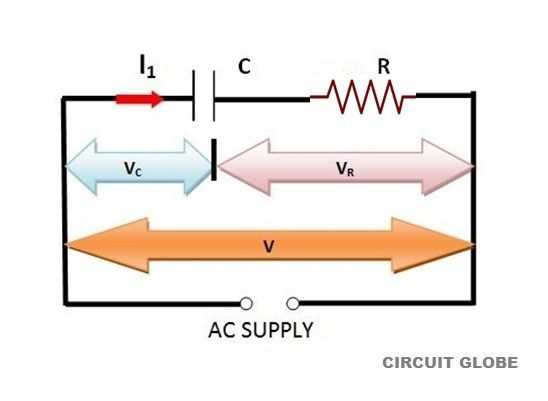
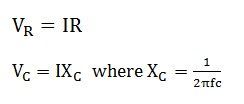Definition: The combination of a pure resistance R in ohms and pure capacitance C in Farads is called RC circuit. The capacitor stores energy and the resistor connected in series with the capacitor controls the charging and discharging of the capacitor. The RC circuit is used in camera flashes, pacemaker, timing circuit etc.
The RC signal filters the signals by blocking some frequencies and allowing others to pass through it. It is also called first-order RC circuit and is used to filter the signals bypassing some frequencies and blocking others. The RC filters are mostly used for selecting signals and for rejecting noise.
The high-pass filter and the low-pass filter are the most common type of RC filters. The high pass filter passes the frequency greater than the fixed cut-off frequency and blocks the frequency lower than the fixed cut-off frequency.
Similarly, the low-pass filter allows the frequency lower than the fixed cut-off frequency and attenuates the frequency higher than the fixed cut-off frequency.
RC Series Circuit
A circuit containing resistance and capacitance connected in series together is called RC series circuit.
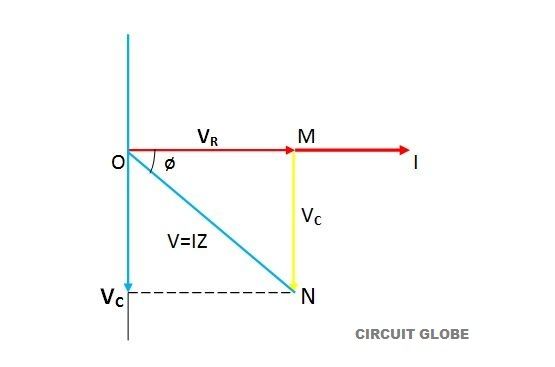
 Steps to draw a phasor diagram for an RC circuit
Steps to draw a phasor diagram for an RC circuit
- Current I is taken as reference
- Voltage drop in resistance is (VR).
VR = IR is drawn in phase with the current I
- Voltage drop in capacitive reactance is (VC).
VC = IXC and is drawn 90° behind the current (as current leads the voltage
by 90° in pure capacitive load circuit).
- The vector sum of the two voltage drops is equal to the applied voltage (V).
Now in right-angle triangle OMN
V = √(VR)2+(VC)2
V = √(IR) 2 + (IXC) 2
V = I √R2 + X2C
I = V/√R2 +X2C = V/Z
Where Z= √R2 +X2C
Z is known as the impedance of the circuit and is defined as the total opposition offered to the flow of current in an RC series circuit. It is measured in ohms.