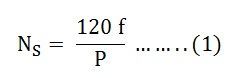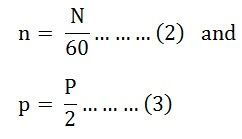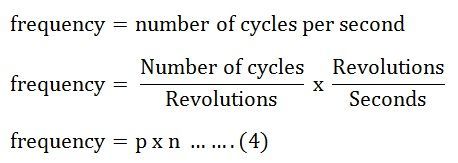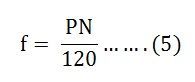The synchronous speed is the speed of the revolution of the magnetic field in the stator winding of the motor. It is the speed at which the electromotive force is produced by the alternating machine. The Synchronous Speed is given by the relation shown below.
The above equation (1) shows that the rotor speed N bears a constant relationship with the field poles and the frequency of the generated voltage in the armature winding. A machine that runs at synchronous speed is called a synchronous machine. Thus, an AC machine in which the rotor moved at a speed and built a constant relationship between the frequency of the voltage in the armature winding and the number of poles is called a Synchronous Machine.
The table below gives the number of poles and synchronous speeds for a power frequency of 50 hertz.
| Number of Poles | Synchronous Speed NS in r.p.m |
|---|---|
| 2 | 3000 |
| 4 | 1500 |
| 6 | 1000 |
| 8 | 750 |
| 10 | 600 |
| 12 | 500 |
Relationship Between Speed and Frequency
The frequency of the generated voltage depends upon the number of field poles and on the speed at which the field poles are rotated. One complete cycle of voltage is generated in an armature coil when a pair of field poles passes over the coil.
Let,
- P be the total number of field poles,
- p is the pair of the field poles,
- N is the speed of the field in revolution per minute (r.p.m),
- n is the field poles in revolution per second (r.p.s), and
- f is the frequency of the generated voltage in hertz.
In one revolution of the rotor, an armature coil is cut by P/2 north poles and P/2 south poles. Since one cycle is generated in an armature coil when a pair of field poles passes over the coil. The number of cycles generated by one revolution of the rotor. Will be equal to the number of pairs of poles. i.e.,
- Number of cycles per revolution = p
- Number of revolutions per second = n
Putting the value of n and p from the equation (2) and (3) in equation (4) we will get
The above equation (3) and (5) gives the relationship between the number of poles, speed, and frequency.