When the system is unbalanced the voltages, currents and the phase impedances are in general unequal. Such a system can be solved by a symmetrical per phase technique, known as the method of symmetrical components. This method is also called a three-component method. The method of symmetrical components simplified the problems of the unbalanced three-phase system. It is used for any number of phases but mainly used for the three-phase system.
The unbalanced three phase system is solved regarding symmetrical components, and then it can be transferred back to the actual circuit. The balanced set of components can be given as a positive sequence component, negative sequence component, and zero phase sequence component.
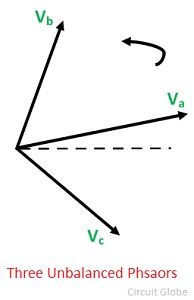
Consider an unbalanced voltage phasor system shown in the figure below. Suppose that the phasors are represented by Va, Vb and Vc and their phase sequence is Va, Vb, and Vc. The phase sequence of the positive component is Va, Vb and Vc and the phase sequence of negative components is Va, Vc, and Vb.
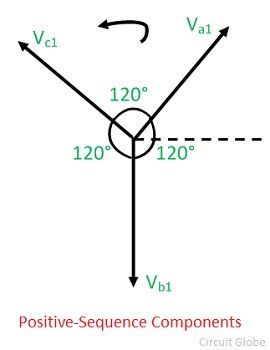
 In positive phase sequence component, the set of three phasors are equal in magnitude, spaced 120° apart from each other and having the same phase sequence as the original unbalanced phasors. The positive sequence component of the unbalanced three phase system is shown below.
In positive phase sequence component, the set of three phasors are equal in magnitude, spaced 120° apart from each other and having the same phase sequence as the original unbalanced phasors. The positive sequence component of the unbalanced three phase system is shown below.
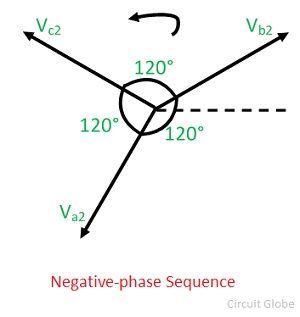
 In negative phase sequence component, the set of the three phasors are equal in magnitude, spaced 120° apart from each other and having the phase sequence opposite to that of the original phasors. The negative phase sequence is shown in the figure below
In negative phase sequence component, the set of the three phasors are equal in magnitude, spaced 120° apart from each other and having the phase sequence opposite to that of the original phasors. The negative phase sequence is shown in the figure below
 In zero phase sequence components, the set of three phasors is equal in magnitude to zero phase displacement from each other. The zero phase sequence component is shown in the figure below.
In zero phase sequence components, the set of three phasors is equal in magnitude to zero phase displacement from each other. The zero phase sequence component is shown in the figure below.
 The three phase balanced system is a special case of a general three-phase system in which zero and negative sequence components are zero.
The three phase balanced system is a special case of a general three-phase system in which zero and negative sequence components are zero.
