The equal area criterion is a simple graphical method for concluding the transient stability of two-machine systems or a single machine against an infinite bus. This principle does not require the swing equation for the determination of stability conditions. The stability conditions are recognized by equating the areas of segments on the power angle diagram between the p-curve and the new power transfer line of the given curve.
The principle of this method consists on the basis that when δ oscillates around the equilibrium point with constant amplitude, transient stability will be maintained.
Starting with swing equation
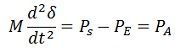 where, M = Angular Momentum
where, M = Angular Momentum
PE = Electrical Power
PS = Mechanical Power
δ= Load Angle
Multiplying both sides of the above equation by dδ/dt, we get
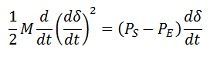 Rearranging, multiplying by dt and integrating, we have
Rearranging, multiplying by dt and integrating, we have
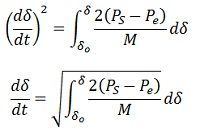 Where δo, is the torque angle at which the machine is operating while running at synchronous speed under normal conditions. Under the above conditions, the torque angle was not changing i.e. before the disturbance.
Where δo, is the torque angle at which the machine is operating while running at synchronous speed under normal conditions. Under the above conditions, the torque angle was not changing i.e. before the disturbance. 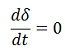 Also, if the system has transient stability the machine will again operate at synchronous speed after the disturbances, i.e.,
Also, if the system has transient stability the machine will again operate at synchronous speed after the disturbances, i.e.,
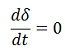 Hence the condition for the transient state stability is given by the equation
Hence the condition for the transient state stability is given by the equation
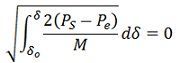
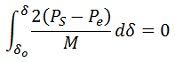
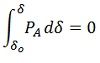
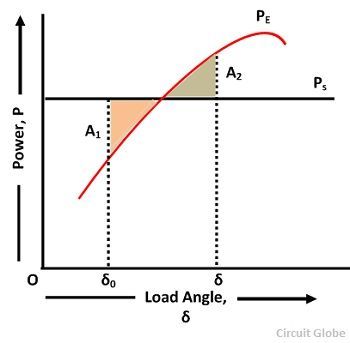 The area A1 represents the kinetic energy stored by the rotor during acceleration, and the A2 represents the kinetic energy given up by the rotor to the system, and when it is all given up, the machine has returned to its original speed.
The area A1 represents the kinetic energy stored by the rotor during acceleration, and the A2 represents the kinetic energy given up by the rotor to the system, and when it is all given up, the machine has returned to its original speed.
The area under the curve PA should be zero, which is possible only when PA has both accelerating and decelerating powers, i.e., for a part of the curve PS> PE and for the other PE> PS. For a generation action, PS> PE for the positive area and A1> PS for negative areas A2 for stable operation. Hence the name equal area criterion.
The equal area criterion is also used for determining the maximum limit on the load that the system can take without exceeding the stability limit. This can happen only when the area between the PS line and the PE curve is equal to the area between the PS line, and the PE curve is equal to the area between the initial torque angle δ0 and the line PS. In this case, the area A2 is less than the area A1; the system will become unstable.
The problems associated with the transient stability of the system is because of the following reasons. These are as follows
- Sudden change in load
- Switching off one of the lines which cause a change in the reactance of the system and hence a change in load conditions.
- Sudden fault on the system which causes the reduction in output, requiring an arrangement for clearance for the clearance of the fault rapidly, and study of after fault condition which may cause part of the system outage.
In each case, the procedure will be to determine the power angle curve for the initial conditions of the system, for the conditions under fault, and for the after fault condition and plot the curve in per unit value. Then locate the points for the load initial conditions finding out δo. Then, using equal area criterion, determine the new angle of displacement δ. The maximum angle δmax which may be allowed and the corresponding maximum permissible load can also be determined

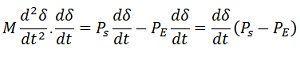
Very good