Definition: The number system whose base is 8 is known as the octal number system. The base 8 means the system uses eight digits from 0 to 7. All the eight digits from 0 to 8 have same physical meaning as that of decimal numbers. The next digit in octal number is represented by 10, 11, 12, 13, 14, 15, 16, 17 which represents the decimal digits 8, 9, 10, 11, 12, 13, 14, 15. In this manner the octal number 20 represents the decimal number 16 and subsequently 21, 22, 23….octal numbers will show the decimal digits 17, 18, 19…etc and so on.
The major disadvantage of the octal number system is that the computer doesn’t understand the octal number system. So the additional circuit is required for the digital systems which convert the octal number to binary number. The octal number system is used in a minicomputer.
Octal to Decimal Conversion
In octal number system, each digit position has the weight eight regarding power eight shown in the figure below.
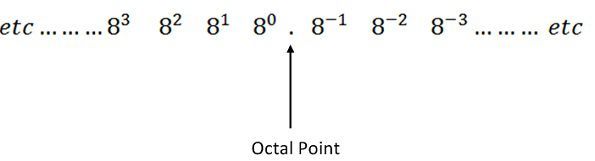
Example – Consider the octal number 354.42 into its equivalent decimal number. The integer part 354 converts to octal shown below.
And the fractional parts 0.42 converts to octal
The decimal number system is 236.53125.
Decimal to Octal Number Conversion
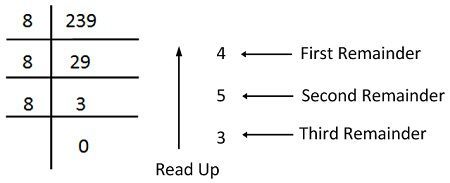
For converting the decimal number into an octal number, the octal dabble method is used. In the octal double method, the integer octal number is divided by the digit 8. And for converting the fractional decimal number into an octal number, it is multiplied by the digit 8 and record the carry. When these carry read down, it gives the fractional octal number.
Example: Consider the conversion of the decimal number 236.53. The conversion of integer part is shown below.
And the fraction part
Thus the octal number is 354.4172.


Very useful information.