Active, Reactive and Apparent Power

Active Power

Definition: The power which is actually consumed or utilised in an AC Circuit is called True power or Active power or Real power. It is measured in kilowatt (kW) or MW. It is the actual outcomes of the electrical system which runs the electric circuits or load.

Reactive Power

Definition: The power which flows back and forth that means it moves in both the directions in the circuit or reacts upon itself, is called Reactive Power. The reactive power is measured in kilo volt-ampere reactive (kVAR) or MVAR.

Apparent Power

Definition: The product of root mean square (RMS) value of voltage and current is known as Apparent Power. This power is measured in kVA or MVA.

It has been seen that power is consumed only in resistance. A pure inductor and a pure capacitor do not consume any power since in a half cycle whatever power is received from the source by these components, the same power is returned to the source. This power which returns and flows in both the direction in the circuit, is called Reactive power. This reactive power does not perform any useful work in the circuit.

In a purely resistive circuit, the current is in phase with the applied voltage, whereas in a purely inductive and capacitive circuit the current is 90 degrees out of phase, i.e., if the inductive load is connected in the circuit the current lags voltage by 90 degrees and if the capacitive load is connected the current leads the voltage by 90 degrees.

Hence, from all the above discussion, it is concluded that the current in phase with the voltage produces true or active power, whereas, the current 90 degrees out of phase with the voltage contributes to reactive power in the circuit.

Therefore,

• True power = voltage x current in phase with the voltage
• Reactive power = voltage x current out of phase with the voltage

The phasor diagram for an inductive circuit is shown below:

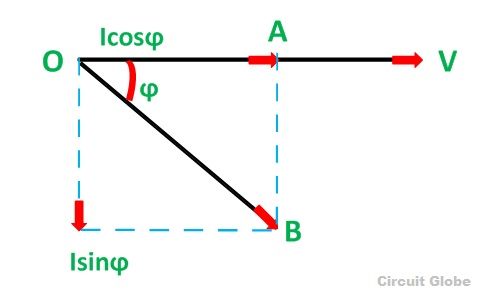Taking voltage V as reference, the current I lags behind the voltage V by an angle ϕ. The current I is divided into two components:

• I Cos ϕ in phase with the voltage V
• I Sin ϕ which is 90 degrees out of phase with the voltage V

Therefore, the following expression shown below gives the active, reactive and apparent power respectively.

• Active power P = V x I cosϕ = V I cosϕ
• Reactive power P_r or Q = V x I sinϕ = V I sinϕ
• Apparent power P_a or S = V x I = VI

Active component of the current

The current component, which is in phase with the circuit voltage and contributes to the active or true power of the circuit, is called an active component or watt-full component or in-phase component of the current.

Reactive component of the current

The current component, which is in quadrature or 90 degrees out of phase to the circuit voltage and contributes to the reactive power of the circuit, is called a reactive component of the current.